题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知a2-b2=2c,且acosB=3bcosA,则边c= .
考点:余弦定理
专题:计算题,解三角形
分析:运用余弦定理,化简acosB=3bcosA,可得2a2=c2+2b2,再由a2-b2=2c,即可得到c的方程,解得即可.
解答:
解:由余弦定理,acosB=3bcosA即为
a•
=3b•
,
即有2a2=c2+2b2,
由于a2-b2=2c,
则4c=c2,
解得,c=4.
故答案为:4.
a•
| c2+a2-b2 |
| 2ac |
| c2+b2-a2 |
| 2bc |
即有2a2=c2+2b2,
由于a2-b2=2c,
则4c=c2,
解得,c=4.
故答案为:4.
点评:本题考查余弦定理及运用,考查运算化简能力,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
|
|=( )
| -5+i |
| 2-3i |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
若将函数f(x)=
sinx-
cosx的图象向右平移m个单位长度,得到的图象关于原点对称,则m=( )
| ||
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知m,n是两条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
| A、若m∥n,n?α,则m平行于平面α内的任意一条直线 |
| B、若m?α,m∥β,n∥β,则α∥β |
| C、若m⊥α,n⊥β,m∥n,则α∥β |
| D、若α∥β,m?α,n?β,则m∥n |
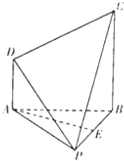 已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.