题目内容
 如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=
如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=| 3 |
(1)求证:AC⊥平面EDB;
(2)求二面角A-EB-C的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得AC⊥BD,DE⊥DC,DE⊥AC,由此能证明AC⊥平面EDB.
(2)以F为原点,FA为x轴,FB为y轴,建立空间直角坐标系,利用向量法能求出二面角A-EB-C的余弦值.
(2)以F为原点,FA为x轴,FB为y轴,建立空间直角坐标系,利用向量法能求出二面角A-EB-C的余弦值.
解答:
(1)证明:∵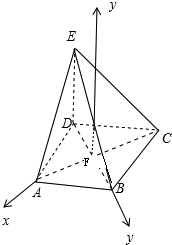 F是菱形ABCD的对角线的交点,
F是菱形ABCD的对角线的交点,
∴AC⊥BD,
∵ED=
,DC=1,EC=2,∠DAB=60°,
∴DE⊥DC,又平面ABCD⊥平面DEC,
∴DE⊥平面ABCD,∴DE⊥AC,
∴AC⊥平面EDB.
(2)以F为原点,FA为x轴,FB为y轴,建立空间直角坐标系,
∵ED=
,DC=1,EC=2,∠DAB=60°,
∴A(
,0,0),E(0,-
,
),
B(0,
,0),C(-
,0,0),
=(
,
,-
),
=(0,1,-
),
=(-
,
,-
),
设平面AEB的法向量
=(x,y,z),
则
,
取z=
,得
=(
,3,
),
设平面CEB的法向量
=(a,b,c),
则
,
取c=
,得
=(-
,3,
),
设二面角A-EB-C的平面角为θ,
cosθ=-|cos<
,
>|=-|
|=-
.
∴二面角A-EB-C的余弦值为-
.
 F是菱形ABCD的对角线的交点,
F是菱形ABCD的对角线的交点,∴AC⊥BD,
∵ED=
| 3 |
∴DE⊥DC,又平面ABCD⊥平面DEC,
∴DE⊥平面ABCD,∴DE⊥AC,
∴AC⊥平面EDB.
(2)以F为原点,FA为x轴,FB为y轴,建立空间直角坐标系,
∵ED=
| 3 |
∴A(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
B(0,
| 1 |
| 2 |
| ||
| 2 |
| EA |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| EB |
| 3 |
| EC |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
设平面AEB的法向量
| n |
则
|
取z=
| 3 |
| n |
| 3 |
| 3 |
设平面CEB的法向量
| m |
则
|
取c=
| 3 |
| m |
| 3 |
| 3 |
设二面角A-EB-C的平面角为θ,
cosθ=-|cos<
| n |
| m |
| -3+9+3 | ||||
|
| 3 |
| 5 |
∴二面角A-EB-C的余弦值为-
| 3 |
| 5 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知数列{an}的各项均为正数,Sn为其前n项的和,且对于任意的n∈N*,都有4Sn=(an+1)2.
(1)求a1,a2的值和数列{an}的通项公式;
(2)求数列bn=
的前n项和Tn.
(1)求a1,a2的值和数列{an}的通项公式;
(2)求数列bn=
| 1 |
| an•an+1 |
设F1、F2是双曲线C:
-
=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2最小内角的大小为30°,则双曲线C的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、x±
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
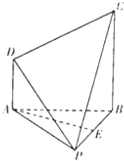 已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.