题目内容

11．已知a＜b＜c，求证：a2b+b2c+c2a＜a2c+b2a+c2b．

分析 由a＜b＜c，可得a-b＜0，b-c＜0，a-c＜0，作差，运用因式分解，以及不等式的性质即可得证．

解答 证明：由a＜b＜c，
可得a-b＜0，b-c＜0，a-c＜0，
a2b+b2c+c2a-（a2c+b2a+c2b）
=（a2b-a2c）+（b2c-bc2）+（c2a-b2a）
=a2（b-c）+bc（b-c）+a（c-b）（c+b）
=（b-c）（a2+bc-ac-ab）
=（b-c）（a-b）（a-c）＜0，
即有a2b+b2c+c2a＜a2c+b2a+c2b．

点评 本题考查不等式的证明，注意运用作差和因式分解，考查运算能力，属于基础题．

练习册系列答案
相关题目
12．已知a＜b，比较1-a3与1-b3的大小．
2．已知函数f（x）=|x2-4x+3|-m有四个零点，则实数m的取值范围是（0，1）．
19．在一个港口，相邻两次高潮发生时间相距12h，低潮时水的深度为8.4m，高潮时为16m．一次高潮发生在10月10日4：00．每天涨潮落潮时，水的深度d（m）与时间t（h）近似满足关系式d=Asin（ωt+φ）+h．
（1）若从10月10日0：00开始计算，求该港口的水深d（m）和时间t（h）之间的函数关系；
（2）10月10日17：00该港口水深约为多少？（精确到0.1m）
（3）10月10日这一天该港口共有多少时间水深低于10.3m？
6．定义域为R的偶函数f（x）满足：对任意x∈R都有f（2-x）=f（x），且当x∈[0，1]时，f（x）=x-1，若函数y=f（x）-loga（x+1）在（0，+∞）上至少有三个零点，则a的取值范围为（　　）
A．（0，$\frac{1}{2}$）B．（$\frac{1}{2}$，1）C．（0，$\frac{1}{3}$）D．（$\frac{1}{3}$，1）
16．定义A*B、B*C、C*D、D*B分别对应下列图形，

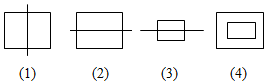
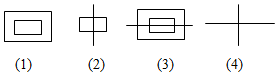
那么下面的图形中，可以表示A*D，A*C的分别是（　　）
A．（1）、（2）B．（2）、（3）C．（2）、（4）D．（1）、（4）
3．为了解某地脐橙种植情况，调研小组在该地某脐橙种植园中随机抽出30棵，每棵挂果情况编成如图所示的茎叶图（单位：个）：若挂果在175个以上（包括175）定义为“高产”，挂果在175个以下（不包括175）定义为“非高产”．
（1）如果用分层抽样的方法从“高产”和“非高产”中抽取5棵，再从这5棵中选2棵，那么至少有一棵是“高产”的概率是多少？
（2）用样本估计总体，若从该地所有脐橙果树（有较多果树）中选3棵，用ξ表示所选3棵中“高产”的个数，试写出ξ的分布列，并求ξ的数学期望．
20．曲线y=$\frac{lnx}{x}$在点（1，0）处的切线是y=x-1．
1．如图是一个几何体的三视图，则在此几何体中，直角三角形的个数是（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网