题目内容
2.已知函数f(x)=|x2-4x+3|-m有四个零点,则实数m的取值范围是(0,1).分析 作出y=|x2-4x+3|的函数图象,令y=|x2-4x+3|图象与直线y=m有四个交点,观察m的取值范围.
解答 解:令f(x)=0得|x2-4x+3|=m,作出y=|x2-4x+3|的函数图象如图所示:
∵f(x)有四个零点,∴y=|x2-4x+3|与直线y=m有四个交点,
由图象可知0<m<1.
故答案为(0,1).
点评 本题考查了函数零点与函数图象的关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知x0是函数f(x)=-2x+$\frac{3}{x}$的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)>0 | D. | f(x1)>0,f(x2)<0 |
12. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )| A. | $\frac{\sqrt{22}}{22}$ | B. | $\frac{\sqrt{22}}{11}$ | C. | $\frac{3\sqrt{22}}{22}$ | D. | $\frac{2\sqrt{22}}{11}$ |
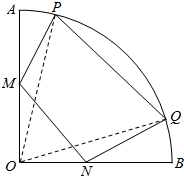 如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.
如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.