题目内容
如图,F1,F2分别是椭圆C: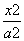 +
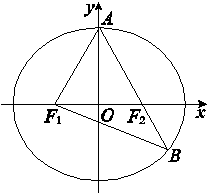
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
(1)求椭圆C的离心率;
 (2)已知△AF1B的面积为40
(2)已知△AF1B的面积为40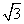 ,求a,b的值.
,求a,b的值.
解: (1)由题意可知,△AF1F2为等边三角形,a=2c,所以e=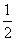 .
.
(2)( 方法一)a2=4c2,b2=3c2.
直线AB的方程可为y=-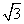 (x-c).
(x-c).
将其代入椭圆方程3x2+4y2=12c2,得B
所以|AB|=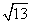 ·
·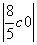 =
=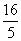 c
c
由S△AF1B=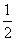 |AF1|·|AB|sin∠F1AB
|AF1|·|AB|sin∠F1AB
=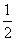 a·
a·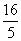 c·
c·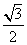 =
=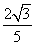 a2=40
a2=40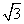 ,
,
解得a=10,b=5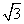 .
.
(方法二)设|AB|=t.
因为|AF2|=a,所以|BF2|=t-a.
由椭圆定义|BF1|+|BF2|=2a可知,|BF1|=3a-t.
再由余弦定理(3a-t)2=a2+t2-2atcos60°可得,
t=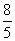 a.
a.
由S△AF1B=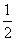 a·
a·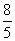 a·
a·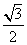 =
=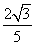 a2=40
a2=40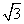 知,a=10,b=5
知,a=10,b=5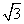 .
.

练习册系列答案
相关题目
 的外接球直径为
的外接球直径为 ,底面边长
,底面边长 ,则侧棱
,则侧棱 与平面
与平面 所成角的正切值为_________。
所成角的正切值为_________。 ,使
,使 ”的否定为 。
”的否定为 。 满足
满足
 ,则
,则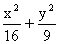 =1上任意一点,则点P到直线 AB距离的最大值是 ______________.
=1上任意一点,则点P到直线 AB距离的最大值是 ______________. ,则
,则 的值为 ;
的值为 ; 、
、 分别为双曲线
分别为双曲线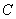 :
:
 的左焦点、右顶点,点
的左焦点、右顶点,点 满足
满足 ,则双曲线的离心率为 ;
,则双曲线的离心率为 ;  -
- =1的焦点到渐近线的距离为( )
=1的焦点到渐近线的距离为( ) B.2 C.
B.2 C. D.1
D.1