题目内容
11.已知x=lnx,y=log52,z=e-0.5,则( )| A. | x<y<z | B. | x<z<y | C. | z<y<x | D. | y<z<x |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵x=lnx>1,y=log52$<lo{g}_{5}\sqrt{5}$=$\frac{1}{2}$,z=e-0.5=$\frac{1}{\sqrt{e}}$$∈(\frac{1}{2},1)$.
∴x>z>y.
故选:D.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.在等比数列{an}中,已知a4=8a1,且a1,a2+1,a3成等差数列.则{an}的前5项和为( )
| A. | 31 | B. | 62 | C. | 64 | D. | 128 |
19.若函数$f(x)=\left\{\begin{array}{l}{a^x},x>1\\(4-\frac{a}{2})x+2,x≤1\end{array}\right.$在(-∞,+∞)上单调递增,则的取值范围是( )
| A. | [4,8) | B. | (1,+∞) | C. | (4,8) | D. | (1,8) |
16.设函数f(x)满足2x2f(x)+x3f′(x)=ex,f(2)=$\frac{{e}^{2}}{8}$,则x∈[2,+∞)时,f(x)( )
| A. | 有最大值$\frac{{e}^{2}}{8}$ | B. | 有最小值$\frac{{e}^{2}}{8}$ | C. | 有最大值$\frac{{e}^{2}}{2}$ | D. | 有最小值$\frac{{e}^{2}}{2}$ |
3.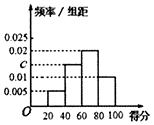 某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
(Ⅰ)求a,b,c的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中选取5人进行座谈.现再从这5人中任选2人,求这两人都合格的概率.
 某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中选取5人进行座谈.现再从这5人中任选2人,求这两人都合格的概率.
17.若|x-s|<t,|y-s|<t,则下列不等式中一定成立的是( )
| A. | |x-y|<2t | B. | |x-y|<t | C. | |x-y|>2t | D. | |x-y|>t |
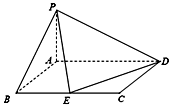 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.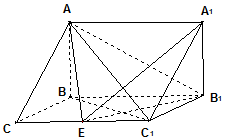 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.