题目内容
正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点N在线段BD1上运动,则M,N两点间的最小距离为: .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:利用空间直线和平面之间的关系证明ME⊥BD1,即可得到结论.
解答:
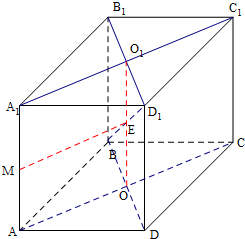 解:连结AC,A1C1,则在正方体ABCD-A1B1C1D1中,
解:连结AC,A1C1,则在正方体ABCD-A1B1C1D1中,
AC⊥平面B1D1DB,
取O1O的中点E,连结ME,则ME∥AC,
则ME⊥平面B1D1DB,
即ME⊥BD1,
若点N在线段BD1上运动,则M,N两点间的最小距离为ME,
∵正方体ABCD-A1B1C1D1的棱长为1,ME=AO,
∴AO=
AC=
,
故M,N两点间的最小距离为:
,
故答案为:
 解:连结AC,A1C1,则在正方体ABCD-A1B1C1D1中,
解:连结AC,A1C1,则在正方体ABCD-A1B1C1D1中,AC⊥平面B1D1DB,
取O1O的中点E,连结ME,则ME∥AC,
则ME⊥平面B1D1DB,
即ME⊥BD1,
若点N在线段BD1上运动,则M,N两点间的最小距离为ME,
∵正方体ABCD-A1B1C1D1的棱长为1,ME=AO,
∴AO=
| 1 |
| 2 |
| ||
| 2 |
故M,N两点间的最小距离为:
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查空间两点间距离的计算,根据直线垂直的性质转化直线垂直是解决本题的关键.

练习册系列答案
相关题目
把正整数按图所示的规律排序,则从2008到2010的箭头方向依次为( )


A、 |
B、 |
C、 |
D、 |
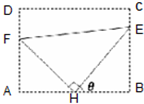 如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10
如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10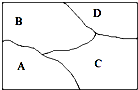 如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有
如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有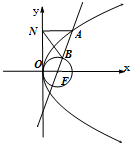 如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,
如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,
