题目内容
若x1,x2,x3,…x30这30个数据的平均数为
,方差为0.31,则x1,x2,x3,…x30,
的方差为( )
. |
| x |
. |
| x |
| A、0.4 | B、0.3 |
| C、0.04 | D、1 |
考点:极差、方差与标准差,众数、中位数、平均数
专题:概率与统计
分析:根据平均数与方差的定义与公式,推导出数据x1,x2,x3,…x30,
的平均数与方差.
. |
| x |
解答:
解:根据题意,∵
=
,
∴x1+x2+x3+…+x30=30
;
又∵s2=
[(x1-
)2+(x2-
)2+(x3-
)2+…+(x30-
)2]=0.31,
∴[(x1-
)2+(x2-
)2+(x3-
)2+…+(x30-
)2]=0.31×30;
∴x1,x2,x3,…x30,
的平均数为
=
=
=
,
方差为s02=
[(x1-
)2+(x2-
)2+(x3-
)2+…+(x30-
)2+(
-
)2]
=
[0.31×30+0]=0.3.
故选:B.
. |
| x |
| x1+x2+x3+…+x30 |
| 30 |
∴x1+x2+x3+…+x30=30
. |
| x |
又∵s2=
| 1 |
| 30 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
∴[(x1-
. |
| x |
. |
| x |
. |
| x |
. |
| x |
∴x1,x2,x3,…x30,
. |
| x |
. |
| x0 |
(x1+x2+x3+…+x30+
| ||
| 31 |
30
| ||||
| 31 |
. |
| x |
方差为s02=
| 1 |
| 31 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| 31 |
故选:B.
点评:本题考查了平均数与方差的应用问题,也考查了一定的推理与计算能力,解题时应根据平均数与方差的定义与公式,进行推导与计算,是基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
甲、乙两种农作物品种连续5季的单位面积平均产量如下(单位:t/hm2),根据这组数据,下列说法正确的是( )
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 4.9 | 4.95 | 5.05 | 5 | 5.1 |
| 乙 | 4.7 | 5.15 | 5.4 | 4.85 | 4.9 |
| A、甲品种的样本平均数大于乙品种的样本平均数 |
| B、甲品种的样本平均数小于乙品种的样本平均数 |
| C、甲品种的样本方差大于乙品种的样本方差 |
| D、甲品种的样本方差小于乙品种的样本方差 |
双曲线
-
=1的焦点到渐近线的距离与顶点到渐近线的距离之比为( )
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
函数y=sinx在点(
,
)处的切线方程是( )
| π |
| 3 |
| ||
| 2 |
A、x+2y-
| ||||
B、x+2y+
| ||||
C、x-2y-
| ||||
D、x-2y+
|
下列函数中,最小值为4的是( )
A、y=x+
| ||
B、y=sinx+
| ||
| C、y=3x+4•3-x | ||
| D、y=log3x+4logx3 |
学校为了了解高二年级教学情况,对清北班、重点班、普通班、艺术班的学生做分层抽 样调查,假设学校高二年级总人数为N,其中清北班有学生144人,若在清北班、重点班、普通班、艺术班抽取的人数分别为18,66,53,24,则总人数N为( )
| A、801 | B、1 288 |
| C、853 | D、912 |
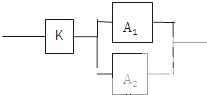 如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )
如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )| A、0.960 | B、0.864 |
| C、0.72 | D、0.576 |