题目内容
椭圆的长轴和短轴把椭圆分成4块,现有5种不同的颜料给4块涂色,要求共边两块颜色互异,每块只涂一色,一共有多少种不同的涂法.
考点:计数原理的应用
专题:概率与统计
分析:如图所示,先给A涂颜色,可有5种不同的涂法;再给B涂颜色,则只有4种涂法;给C涂颜色,若与A相同,则只有一种涂法,此时D可有4种不同涂法;给C涂颜色,若与A不相同,则有3种涂法,此时D可有3种不同涂法.再根据计数原理即可得出.
解答:
解:如图所示,
先给A涂颜色,可有5种不同的涂法;再给B涂颜色,则只有4种涂法;给C涂颜色,若与A相同,则只有一种涂法,此时D可有4种不同涂法;给C涂颜色,若与A不相同,则有3种涂法,此时D可有3种不同涂法.
根据计数原理可得:5×4×1×4+5×4×3×3=260.
故一共有260种不同的涂法.

先给A涂颜色,可有5种不同的涂法;再给B涂颜色,则只有4种涂法;给C涂颜色,若与A相同,则只有一种涂法,此时D可有4种不同涂法;给C涂颜色,若与A不相同,则有3种涂法,此时D可有3种不同涂法.
根据计数原理可得:5×4×1×4+5×4×3×3=260.
故一共有260种不同的涂法.
点评:本题考查了计数原理的应用,考查了分类讨论的思想方法,考查了推理能力,属于基础题.

练习册系列答案
相关题目
tan
等于( )
| 5π |
| 6 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
过抛物线y2=4x的顶点O作互相垂直的两弦OM,ON,则M的横坐标x1与N的横坐标x2之积为( )
| A、64 | B、32 | C、16 | D、4 |
已知数列{an}的前n项和Sn=2n-1,n=1,2,3,…,那么数列{an}( )
| A、是等差数列但不是等比数列 |
| B、是等比数列但不是等差数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列也不是等比数列 |
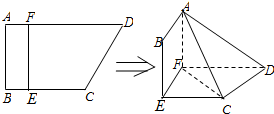 (文科做)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F分别在BC,AD上,EF∥AB现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.
(文科做)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F分别在BC,AD上,EF∥AB现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.