题目内容
2.下列命题中错误的是( )| A. | 命题“若 x2-5x+6=0,则x=2”的逆否命题是“若 x≠2,则x2-5x+6≠0” | |
| B. | 命题“角α的终边在第一象限,则α是锐角”的逆命题为真命题 | |
| C. | 已知命题 p和 q,若p∨q 为假命题,则命题 p与q中必一真一假 | |
| D. | 命题“若x>y,则 x>|y|”的逆命题是真命题 |
分析 写出原命题的逆否命题,可判断A;写出原命题的逆命题,可判断B,D;根据命题命题真假判断的真值表,可判断C.
解答 解:命题“若 x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0”,故A正确;
命题“角α的终边在第一象限,则α是锐角”的逆命题为“α是锐角,则角α的终边在第一象限”,是真命题,故B正确;
已知命题 p和 q,若p∨q 为假命题,则命题 p与q全是假命题,故C错误;
命题“若x>y,则 x>|y|”的逆命题是“若x>|y|,则 x>y”,是真命题,故D正确;
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,复合命题,难度中档.

练习册系列答案
相关题目
12.已知i是虚数单位,复数$\frac{2i}{1+i}$的值为( )
| A. | 1-i | B. | 1+i | C. | i | D. | 2-i |
10.在矩形ABCD中,$\overrightarrow{AB}=({1,-3}),\overrightarrow{AC}=({k,-2})$,则实数k=( )
| A. | -5 | B. | -4 | C. | $\frac{2}{3}$ | D. | 4 |
17.如图正六边形ABCDEF的边长为1,点G是边AF的中点,则$\overrightarrow{BD}•\overrightarrow{BG}$=( )
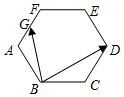

| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{7\sqrt{3}}}{8}$ |
7.已知函数 f(x)=$\left\{\begin{array}{l}{-2x(-1≤x≤0)}\\{\sqrt{x}(0<x≤1)}\end{array}\right.$,则下列图象正确的是( )
| A. | 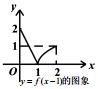 | B. | 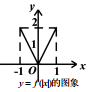 | C. | 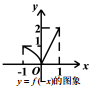 | D. | 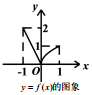 |
11.已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足2|$\overrightarrow{a}$|=3|$\overrightarrow{b}$|,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
1. 如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )
如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )
 如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )
如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )| A. | 对任意的点P,都有T(S6(P))=T(P) | |
| B. | 至少存在4个单位圆上的P,使得T(S3(P))=T(P) | |
| C. | 若点P的坐标为(1,0),则有T(S(P))=$\frac{\sqrt{3}}{2}$ | |
| D. | 对任意的点P,都有T(P)+T(S2(P))+T(S4(P))=0 |