题目内容
圆与椭圆有很多类似的性质，如圆的面积为πr2（r为圆的半径），椭圆的面积为πab（a，b分别为椭圆的长、短半轴的长）．某同学研究了下面几个问题：
（1）圆x2+y2=r2上一点（x0，y0）处的切线方程为x0x+y0y=r2，类似地，请给出椭圆
+
=1（a＞b＞0）上一点（x0，y0）处的切线方程（不必证明）；
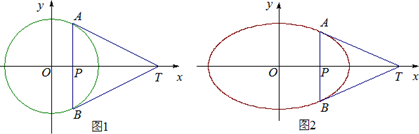
（2）如图1，TA，TB为圆x2+y2=r2的切线，A，B为切点，OT与AB交于点P，则OP•OT=r2．如图2，TA，TB为椭圆
+
=1（a＞b＞0）上的切线，A，B为切点，OT与AB交于点P，请给出椭圆中的类似结论并证明．
（3）若过椭圆
+
=1（a＞b＞0）上外一点M（s，t）作两条直线与椭圆切于A，B两点，且AB恰好过椭圆的左焦点，求证：点M在一条定直线上．
（1）圆x2+y2=r2上一点（x0，y0）处的切线方程为x0x+y0y=r2，类似地，请给出椭圆
| x2 |
| a2 |
| y2 |
| b2 |
（2）如图1，TA，TB为圆x2+y2=r2的切线，A，B为切点，OT与AB交于点P，则OP•OT=r2．如图2，TA，TB为椭圆
| x2 |
| a2 |
| y2 |
| b2 |
（3）若过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）椭圆
+
=1(a＞b＞0)上一点（x0，y0）处的切线方程为
+
=1．
（2）TA，TB为椭圆
+
=1(a＞b＞0)的切线，A，B为切点，OT与AB交于点P，则OP•OT=a2．设A（x0，y0），则直线AT的方程为
+
=1．令y=0，得点T的坐标为(
，0)，由此能证明OP•OT=a2．
（3）设A（x1，y1），B（x2，y2），则点A处的切线方程为
+
=1，点B处的切线方程为
+
=1，由此求出直线AB的方程，由直线AB过椭圆的左焦点，能证明点M在椭圆的左准线上．
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
（2）TA，TB为椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
| a2 |
| x0 |
（3）设A（x1，y1），B（x2，y2），则点A处的切线方程为
| x1x |
| a2 |
| y1y |
| b2 |
| x2x |
| a2 |
| y2y |
| b2 |
解答：
（1）解：椭圆
+
=1(a＞b＞0)上一点（x0，y0）处的切线方程为
+
=1…（2分）
（2）解：如图2，TA，TB为椭圆
+
=1(a＞b＞0)的切线，A，B为切点，
OT与AB交于点P，则OP•OT=a2…（4分）
证明：设A（x0，y0），则直线AT的方程为
+
=1．
令y=0，得x=
，∴点T的坐标为(
，0)…（6分）
又点P的坐标为（x0，0），∴OP•OT=|
|•|x0|=a2…（8分）
（3）证明：设A（x1，y1），B（x2，y2），
则点A处的切线方程为
+
=1，点B处的切线方程为
+
=1…（10分）
将点M（s，t）代入，得
，
∴直线AB的方程为
+
=1…（14分）
又∵直线AB过椭圆的左焦点，∴-
=1，则s=-
，
∴点M在椭圆的左准线上．…（16分）
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
（2）解：如图2，TA，TB为椭圆
| x2 |
| a2 |
| y2 |
| b2 |
OT与AB交于点P，则OP•OT=a2…（4分）
证明：设A（x0，y0），则直线AT的方程为
| x0x |
| a2 |
| y0y |
| b2 |
令y=0，得x=
| a2 |
| x0 |
| a2 |
| x0 |
又点P的坐标为（x0，0），∴OP•OT=|
| a2 |
| x0 |
（3）证明：设A（x1，y1），B（x2，y2），
则点A处的切线方程为
| x1x |
| a2 |
| y1y |
| b2 |
| x2x |
| a2 |
| y2y |
| b2 |
将点M（s，t）代入，得
|
∴直线AB的方程为
| sx |
| a2 |
| ty |
| b2 |
又∵直线AB过椭圆的左焦点，∴-
| sc |
| a2 |
| a2 |
| c |
∴点M在椭圆的左准线上．…（16分）
点评：本题考查切线方程的求法，考查类似结论的叙述并证明，考查点在椭圆左准线上的证明，解题时要认真审题，注意类比猜想能力的培养．
练习册系列答案
相关题目
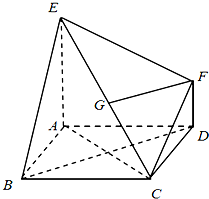如图，已知多面体EABCDF的底面ABCD是正方形，EA⊥底面ABCD，FD∥EA，且EA=2FD．
如图，在△ABC中，AB=4，AC=1，∠BAC=60°．
如图，四棱锥P-ABCD的底面ABCD是边长为2的菱形，∠BAD=60°．已知PB=PD=2，PA=