题目内容
对于平面α、β、γ和直线a、b、m、n,下列命题中真命题是( )
| A、若α∥β,α∩γ=a,β∩γ=b,则a∥b |
| B、若a∥b,b?α,则a∥α |
| C、若a⊥m,a⊥n,m?α,n?α,则a⊥α |
| D、若α⊥β,a?α,则a⊥β |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:由面面平行的性质定理可判断A;由线面平行的判定定理可判断B;由线面垂直的判定定理可判断C;由面面垂直的性质定理可判断D.
解答:
解:若α∥β,α∩γ=α,β∩γ=b,则由面面平行的性质定理可得:a∥b,故A正确;
若a∥b,b?α,则a∥α或a?α,故B错误;
若a⊥m,a⊥n,m?α,n?α,则m,n相交时a⊥α,否则a⊥α不一定成立,故C错误;
若α⊥β,a?α,则a与β可能平行,可能垂直,也可能线在面内,故D错误;
故选:A
若a∥b,b?α,则a∥α或a?α,故B错误;
若a⊥m,a⊥n,m?α,n?α,则m,n相交时a⊥α,否则a⊥α不一定成立,故C错误;
若α⊥β,a?α,则a与β可能平行,可能垂直,也可能线在面内,故D错误;
故选:A
点评:本题考查的知识点是空间中直线与直线之间的位置关系,熟练掌握空间线面关系的判定理,性质定理和几何特征,是解答的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、a?α,b?β,则a与b是异面直线 |
| B、a与b异面,b与c异面,则a与c异面 |
| C、a,b不同在平面α内,则a与b异面 |
| D、a,b不同在任何一个平面内,则a与b异面 |
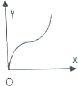
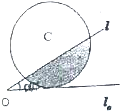 如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )
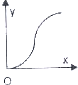
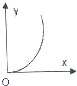
如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )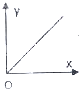
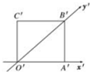 如图,正方形O′A′B′C′的边长为acm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是
如图,正方形O′A′B′C′的边长为acm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是 如图,已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x,y的正半轴上(含原点)滑动,则
如图,已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x,y的正半轴上(含原点)滑动,则