题目内容
已知△ABC的三边长|AB|= ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ +μ
+μ ,且λμ=
,且λμ=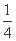 .
.

(1)求| |最小值,并指出此时
|最小值,并指出此时 与
与 ,
, 的夹角;
的夹角;
(2)是否存在两定点F1,F2使|| |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
解:(1)由余弦定理知:
cos∠ACB= =
=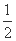 ⇒∠ACB=
⇒∠ACB= .
.
因为| |2 =
|2 = =(λ
=(λ +μ
+μ )2
)2
=λ2+16μ2+2λμ ·
·
=λ2+16μ2+1≥3.
所以| |≥
|≥ ,当且仅当λ=±1时,“=”成立.
,当且仅当λ=±1时,“=”成立.
故| |的最小值是
|的最小值是 ,
,
此时 < ,
, >=<
>=< ,
, >=
>= 或
或 .
.
(2)以C为坐标原点,∠ACB的平分线所在直线为x轴建立直角坐标系(如图),则A ,B(2
,B(2 ,-2),
,-2),
设动点M(x,y),

因为 =λ
=λ +μ
+μ ,
,
所以 ⇒
⇒
再由λμ=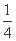 知
知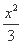 -y2=1,
-y2=1,
所以,动点M的轨迹是以F1(-2,0),F2(2,0)为焦点,实轴长为2 的双曲线,
的双曲线,
即存在两定点F1(-2,0),F2(2,0)使|| |-|
|-| ||恒为常数2
||恒为常数2 ,即k=2
,即k=2 .
.

练习册系列答案
相关题目
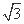 cos x(0≤x<2π)取得最大值时,x= .
cos x(0≤x<2π)取得最大值时,x= . 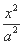 -
-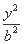 =1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 . 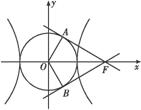
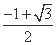 (B)
(B)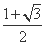
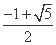 (D)
(D)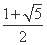
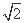 x (B)y=±
x (B)y=± x
x +
+ =1的中心和左焦点,点P为椭圆上的任意一点,则
=1的中心和左焦点,点P为椭圆上的任意一点,则 ·
· 的最大值为( )
的最大值为( ) (B)
(B)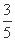 (C)
(C) (D)
(D)
 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3. -
- =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )