题目内容
过双曲线 -
- =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
(A)x±y=0 (B)2x±y=0
(C)4x±y=0 (D)x±2y=0
B
解析:如图所示,设双曲线的另一个焦点为F′,连结OT、PF′.

∵FT为圆的切线,
∴FT⊥OT,且|OT|=a,
又∵T、O分别为FP、FF′的中点,
∴OT∥PF′且|OT|= |PF′|,
|PF′|,
∴|PF′|=2a,
且PF′⊥PF.
又|PF|-|PF′|=2a,
∴|PF|=4a.
在Rt△PFF′中,|PF|2+|PF′|2=|FF′|2,
即16a2+4a2=4c2,
∴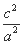 =5.
=5.
∴ =
=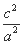 -1=4,
-1=4,
∴ =±2,
=±2,
即渐近线方程为y=±2x,
即2x±y=0.故选B.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ +μ
+μ ,且λμ=
,且λμ=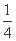 .
.
 |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.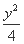 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )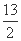 (B)a2=13
(B)a2=13 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
.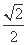 ,求圆P的方程.
,求圆P的方程. +
+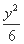 =1和C2:x2-
=1和C2:x2-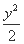 =1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:
=1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:  =
= +m(
+m( +
+ ),则实数m的值为 .
),则实数m的值为 . 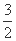 x (B)y=±
x (B)y=±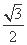 x
x x (D)y=±
x (D)y=±