题目内容
8.定义在实数集R上的函数f(x),满足f(x)=f(2-x)=f(x-2),当x∈[0,1]时,f(x)=x•2x.则函数g(x)=f(x)-|lgx|的零点个数为( )| A. | 99 | B. | 100 | C. | 198 | D. | 200 |
分析 判断f(x)的对称性和周期,做出y=f(x)和y=|lgx|的函数图象,根据两图象的变化规律判断交点个数,从而得出结论.
解答 解:∵f(x)=f(x-2),∴f(x)是以2为周期的函数,
又f(2-x)=f(x-2),∴f(x)是偶函数,
∵f(x)=f(2-x),∴f(x)的图象关于直线x=1对称,
令g(x)=0得f(x)=|lgx|,
做出y=f(x)和y=|lgx|的函数图象如图所示: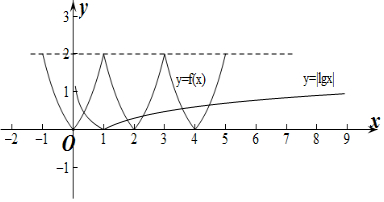
令lgx=2得x=100,
由图象可得y=f(x)和y=|lgx|的函数图象在每个区间[n-1,n]上都有1个交点,n=1,2,3,…,100.
∴g(x)共有100个零点.
故选B.
点评 本题考查了函数零点个数与函数图象的关系,函数周期性,对称性的应用,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16.已知i为虚数单位,复数$z={(\frac{i-1}{i+1})^3}$,则z=( )
| A. | -i | B. | i | C. | 1+i | D. | -1+i |
17.已知a=$\frac{1}{3}$ln$\frac{9}{4}$,b=$\frac{4}{5}$ln$\frac{5}{4}$,c=$\frac{1}{4}$ln4,则下列各式正确的是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
 如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.
如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.