题目内容
19. 如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.
如图,在三棱柱ABC-A1B1C1中,G为△ABC的重心,$BE=\frac{1}{3}B{C_1}$.(1)求证:GE∥平面ABB1A1;
(2)若侧面ABB1A1⊥底面ABC,∠A1AB=∠BAC=60°,AA1=AB=AC=2,求直线A1B与平面B1GE所成角θ的正弦值.
分析 (1)连结CG交AB于O,过G作GD∥AB交BC于D,连结DE,GE,根据重心的性质得出$\frac{BD}{BC}=\frac{OG}{OC}=\frac{1}{3}$,故而可证平面DGE∥平面ABB1A1,从而得出GE∥平面ABB1A1;
(2)连结A1O,可证A1O⊥平面ABC,以O为原点建立空间直角坐标系,求出$\overrightarrow{{A}_{1}B}$和平面B1GE的法向量$\overrightarrow{n}$的坐标,即可得出结论.
解答 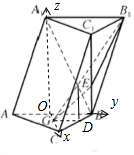 证明:(1)连结CG交AB于O,过G作GD∥AB交BC于D,连结DE,GE
证明:(1)连结CG交AB于O,过G作GD∥AB交BC于D,连结DE,GE
∵G是△ABC的重心,∴$\frac{BD}{BC}=\frac{OG}{OC}=\frac{1}{3}$,
又$BE=\frac{1}{3}B{C_1}$,∴DE∥CC1,
∴DE∥BB1,
又GD∥AB,GD∩DE=D,AB∩BB1=B,
∴平面GDE∥平面ABB1A1,
∵GE?平面ABB1A1,
∴GE∥平面ABB1A1.
(2)连结AO,
∵AA1=2,AO=$\frac{1}{2}AB$=1,∠A1AB=60°,
∴A1O=$\sqrt{4+1-2}$=$\sqrt{3}$.
∴AO2+A1O2=AA12,∴A1O⊥AB.
∵侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,A1O?平面ABB1A1,
∴A1O⊥平面ABC.
∵AB=AC,∠BAC=60°,∴△ABC是等边三角形,
∴OC⊥AB,
以O为原点,以OC,OB,OA1为坐标轴建立空间直角坐标系,如图所示:
则A1(0,0,$\sqrt{3}$),B(0,1,0),G($\frac{\sqrt{3}}{3}$,0,0),B1(0,2,$\sqrt{3}$),C1($\sqrt{3}$,1,$\sqrt{3}$),
∴$\overrightarrow{{A}_{1}B}$=(0,1,-$\sqrt{3}$),$\overrightarrow{G{B}_{1}}$=(-$\frac{\sqrt{3}}{3}$,2,$\sqrt{3}$),$\overrightarrow{B{C}_{1}}$=($\sqrt{3}$,0,$\sqrt{3}$),$\overrightarrow{GB}$=(-$\frac{\sqrt{3}}{3}$,1,0),
∴$\overrightarrow{GE}$=(0,1,$\frac{\sqrt{3}}{3}$).
设平面B1GE的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{3}x+2y+\sqrt{3}z=0}\\{y+\frac{\sqrt{3}}{3}z=0}\end{array}\right.$,
令z=$\sqrt{3}$得$\overrightarrow{n}$=($\sqrt{3}$,-1,$\sqrt{3}$).
∴sinθ=|$\frac{-1-3}{\sqrt{1+3}•\sqrt{3+1+3}}$|=$\frac{2\sqrt{7}}{7}$.
点评 本题考查了线面平行的判断,空间向量的应用与线面角的计算,属于中档题.

| A. | an=4×($\frac{3}{2}$)n | B. | an=4×($\frac{3}{2}$)n-1 | C. | an=4×($\frac{2}{3}$)n | D. | an=4×($\frac{2}{3}$)n-1 |
| A. | (2,+∞) | B. | (-4,+∞) | C. | (-2,+∞) | D. | (-4,-2)∪(2,+∞) |