题目内容
3.过正方体ABCD-A1B1C1D1的顶点A作直线,使与直线AD1所成的角为30°,且与平面C1D1C所成的角为60°,则这样的直线的条数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 如图所示,在平面C1D1C内,以点D为圆心,半径为$\frac{\sqrt{3}}{3}$AD画圆,则点A与此圆上的点的连线满足条件.
解答 解:如图所示,在平面C1D1C内,以点D为圆心,半径为$\frac{\sqrt{3}}{3}$AD画圆,
则点A与此圆上的点的连线满足:与平面C1D1C所成的角为60°.
所以满足l与直线AD1所成的角为30°有且只有2条,
故选:B.
点评 本题考查了正方体的性质、空间角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.若将函数y=2cos2x的图象向右平移$\frac{π}{12}$个单位长度,则平移后函数的一个零点是( )
| A. | ($\frac{5}{6}$π,0) | B. | ($\frac{7π}{6}$,0) | C. | (-$\frac{π}{3}$,0) | D. | ($\frac{π}{6}$,0) |
8.定义在实数集R上的函数f(x),满足f(x)=f(2-x)=f(x-2),当x∈[0,1]时,f(x)=x•2x.则函数g(x)=f(x)-|lgx|的零点个数为( )
| A. | 99 | B. | 100 | C. | 198 | D. | 200 |
13.已知实数a,b,c满足不等式0<a<b<c<1,且M=2a,N=3-b,P=lnc,则M,N,P的大小关系是( )
| A. | P<N<M | B. | P<M<N | C. | M<P<N | D. | N<P<M |
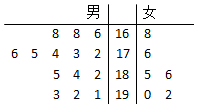 M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.