题目内容

椭圆5x2+ky2=5的一个焦点是（0，-2），则k的值为（　　）
A、1
B、-1
C、
5
D、-
5
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：把椭圆化为标准方程后，找出a与b的值，然后根据a2=b2+c2，表示出c，并根据焦点坐标求出c的值，两者相等即可列出关于k的方程，求出方程的解即可得到k的值．
解答： 解：把椭圆方程化为标准方程得：x2+
y2
5
k
=1，
因为焦点坐标为（0，-2），所以长半轴在y轴上，
则c=
5
k
-1
=2，解得k=1．
故选：A．
点评：此题考查学生掌握椭圆的简单性质化简求值，是基础题．
练习册系列答案
相关题目
对大于或等于2的自然数，m的n次方幂有如下分解分式：
22=1+3，32=1+3+5，42=1+3+5+7；
23=3+5，33=7+9+11，43=13+15+17+19；
根据上述分解规律，若n2=1+3+5+…+21，m3的分解式中最小的数是21，则m+n=
 
．
设函数f（x）=
x2-4x+6，x≥0
x+6，x＜0
，则不等式f（x）＞f（1）的解集是
 
．
正方体A1B1C1D1-ABCD中，AB与B1D1成的角是（　　）
A、30°B、45°
C、60°D、90°
若α是第二象限角，sin
α
2
=
4
5
，则sinα=（　　）
A、
9
25
B、
21
25
C、
24
25
D、-
24
25
抛掷红、黄两颗骰子，当红色骰子的点数为4或6时，两颗骰子的点数之积大于20的概率是（　　）
A、
1
4
B、
1
3
C、
1
2
D、
3
5
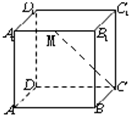如图，在正方体ABCD-A1B1C1D1中，M为A1B1的中点，则MC与平面ABCD所成角的正弦值等于（　　）
A、
2
3
B、
5
3
C、
2
5
5
D、
3
3
在约束条件
x≤1
y≤2
x+y-1≥0
下，目标函数z=ax+by（a＞0，b＞0）的最大值为
1
4
，则ab的最大值为（　　）
A、32
B、64
C、
1
64
D、
1
128
已知等差数列{an}的前n项和为Sn，且S3=6，则5a1+a7的值为（　　）
A、12B、10C、24D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网