Question

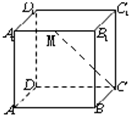如图，在正方体ABCD-A₁B₁C₁D₁中，M为A₁B₁的中点，则MC与平面ABCD所成角的正弦值等于（　　）

• A、

  2

  3

• B、

  5

  3

• C、

  2 5

  5

• D、

  3

  3

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：设正方体的棱长为2，以D为原点，DA为x轴，DC为y轴，利用向量法能求出MC与平面ABCD所成角的正弦值．

解答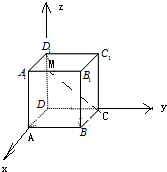： 解：设正方体的棱长为2，以D为原点，DA为x轴，DC为y轴，
DD₁为z轴，建立空间直角坐标系，
则M（2，1，2），C（0，2，0），

CM

=（2，-1，2），
设MC与平面ABCD所成角为θ，
∵平面ABCD的法向量

n

=(0，0，1)，
∴sinθ=|cos＜

CM

，

n

＞|=|

2

9

|=

2

3

．
∴MC与平面ABCD所成角的正弦值为

2

3

．
故选：A．

点评：本题考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意向量法的合理运用．