题目内容
对大于或等于2的自然数,m的n次方幂有如下分解分式:
22=1+3,32=1+3+5,42=1+3+5+7;
23=3+5,33=7+9+11,43=13+15+17+19;
根据上述分解规律,若n2=1+3+5+…+21,m3的分解式中最小的数是21,则m+n= .
22=1+3,32=1+3+5,42=1+3+5+7;
23=3+5,33=7+9+11,43=13+15+17+19;
根据上述分解规律,若n2=1+3+5+…+21,m3的分解式中最小的数是21,则m+n=
考点:归纳推理
专题:推理和证明
分析:根据23=3+5,33=7+9+11,43=13+15+17+19,可知从23起,m3的分解规律恰为数列3,5,7,9,若干连续项之和,23为前两项和,33为接下来三项和,故m3的首数为m2-m+1,利用条件可解.
解答:
解:根据23=3+5,33=7+9+11,43=13+15+17+19,
从23起,m3的分解规律恰为数列3,5,7,9,若干连续项之和,23为前两项和,33为接下来三项和,
故m3的首数为m2-m+1
∵m3(m∈N*)的分解中最小的数是21,
∴m2-m+1=21
∴m=5.
∵n2=1+3+5+…+21=
=11×11,
∴n=11,
∴m+n=5+11=16
故答案为:16,
从23起,m3的分解规律恰为数列3,5,7,9,若干连续项之和,23为前两项和,33为接下来三项和,
故m3的首数为m2-m+1
∵m3(m∈N*)的分解中最小的数是21,
∴m2-m+1=21
∴m=5.
∵n2=1+3+5+…+21=
| 11×(1+21) |
| 2 |
∴n=11,
∴m+n=5+11=16
故答案为:16,
点评:本题考查归纳推理,求解的关键是根据归纳推理的原理归纳出结论,其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
椭圆5x2+ky2=5的一个焦点是(0,-2),则k的值为( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
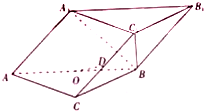 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.