题目内容
已知动点P（x，y）在椭圆C：
+
=1上，F为椭圆C的右焦点，若点M满足|MF|=1．且MP⊥MF，则线段|PM|的最小值为 ．
| x2 |
| 25 |
| y2 |
| 16 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：依题意知，该椭圆的焦点F（3，0），点M在以F（3，0）为圆心，1为半径的圆上，当PF最小时，切线长PM最小，作出图形，即可得到答案．
解答：
解：依题意知，点M在以F（3，0）为圆心，1为半径的圆上，PM为圆的切线，
∴当PF最小时，切线长PM最小．
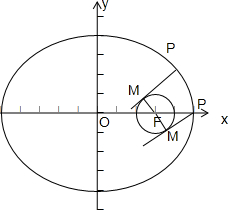
由图知，当点P为右顶点（5，0）时，|PF|最小，最小值为：5-3=2．
此时|PM|=
=
故答案为：
∴当PF最小时，切线长PM最小．
由图知，当点P为右顶点（5，0）时，|PF|最小，最小值为：5-3=2．
此时|PM|=
| 22-12 |
| 3 |
故答案为：
| 3 |
点评：本题考查椭圆的标准方程、圆的方程，考查作图与分析问题解决问题的能力，属于中档题．
练习册系列答案
相关题目
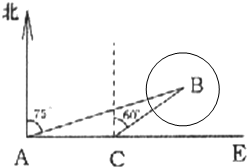如图，海中有一小岛B，周围3.8海里内有暗礁．一军舰从A地出发由西向东航行，望见小岛B在北偏东75°，航行8海里到达C处，望见小岛B在北偏东60°．向量
=（1，2），
=（1，-λ），在区间[-5，5]上随机取一个数λ，使向量2
+
与
-
的夹角为锐角的概率为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|