题目内容
已知函数f(x)=(ax2+x-1)ex,其中e是自然对数的底数,a∈R.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=-1,函数f(x)的图象与函数g(x)=
x3+
x2+m的图象有3个不同的交点,求实数m的取值范围.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=-1,函数f(x)的图象与函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程,函数零点的判定定理,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(Ⅰ)求出导数,求出切线的斜率,切点,运用点斜式方程,即可得到;
(Ⅱ)令h(x)=f(x)-g(x),求出导数,求出单调区间,和极值,函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,即有h(-1)<0,且h(0)>0,解出即可.
(Ⅱ)令h(x)=f(x)-g(x),求出导数,求出单调区间,和极值,函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,即有h(-1)<0,且h(0)>0,解出即可.
解答:
解:(Ⅰ)∵f(x)=(x2+x-1)ex,
∴f′(x)=(2x+1)ex+(x2+x-1)ex=(x2+3x)ex.
∴曲线f(x)在点(1,f(1))处的切线斜率k=f′(1)=4e,
∵f(1)=e,
∴曲线f(x)在点(1,f(1))处的切线方程为y-e=4e(x-1),
即4ex-y-3e=0.
(Ⅱ)令h(x)=f(x)-g(x)=(-x2+x-1)ex-(
x3+
x2+m)
则h′(x)=(-2x+1)ex+(-x2+x-1)ex-(x2+x)
=-(ex+1)(x2+x)
令h′(x)>0得-1<x<0,令h′(x)<0得x>0或x<-1.
∴h(x)在x=-1处取得极小值h(-1)=-
-
-m,在x=0处取得极大值h(0)=-1-m,
∵函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,
∴
即
,
解得:-
-
<m<-1.
∴f′(x)=(2x+1)ex+(x2+x-1)ex=(x2+3x)ex.
∴曲线f(x)在点(1,f(1))处的切线斜率k=f′(1)=4e,
∵f(1)=e,
∴曲线f(x)在点(1,f(1))处的切线方程为y-e=4e(x-1),
即4ex-y-3e=0.
(Ⅱ)令h(x)=f(x)-g(x)=(-x2+x-1)ex-(
| 1 |
| 3 |
| 1 |
| 2 |
则h′(x)=(-2x+1)ex+(-x2+x-1)ex-(x2+x)
=-(ex+1)(x2+x)
令h′(x)>0得-1<x<0,令h′(x)<0得x>0或x<-1.
∴h(x)在x=-1处取得极小值h(-1)=-
| 3 |
| e |
| 1 |
| 6 |
∵函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,
∴
|
|
解得:-
| 3 |
| e |
| 1 |
| 6 |
点评:本题考查导数的运用:求切线方程和求单调区间、极值和最值,考查构造函数,运用导数求极值,考虑极值的正负来判断函数的零点,属于中档题.

练习册系列答案
相关题目
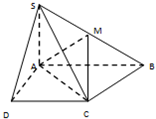 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=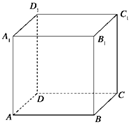 如图已知正方体ABCD-A1B1C1D1的棱长为3,点M在AC上,点N在BC1上,且|AM|=2|MC|,|BN|=2|NC|.
如图已知正方体ABCD-A1B1C1D1的棱长为3,点M在AC上,点N在BC1上,且|AM|=2|MC|,|BN|=2|NC|.