题目内容
4.存在函数f(x)满足对于任意x∈R都有( )| A. | f(|x|)=x+1 | B. | f(x2)=2x+1 | C. | f(|x|)=x2+2 | D. | f($\sqrt{x}$)=3x+2 |
分析 在A、B中,分别取x=±1,由函数性质能排除选项A和B;对于D,x<0,$\sqrt{x}$无意义排除D.
解答 解:对于A,当x=1时,f(1)=2,x=-1时,f(1)=0,不符合题意;
对于B,当x=1时,f(1)=3,x=-1时,f(1)=-1,不符合题意;
对于D,x<0,$\sqrt{x}$无意义,不符合题意.
故选:C.
点评 本题考查了函数的定义的理解,及利用取特殊值对选项进行排除,属于基础题..

练习册系列答案
相关题目
15.已知△ABC的外接圆的圆心为O,AB=2,AC=3,BC=4,则$\overrightarrow{AO}$•$\overrightarrow{BC}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 7 |
9.下列函数中既是偶函数,最小正周期又是π的是( )
| A. | y=sin2x | B. | y=cosx | C. | y=tanx | D. | y=|tanx| |
14.命题“若a=-2b,则a2=4b2”的逆命题是( )
| A. | 若a≠-2b,则a2≠4b2 | B. | 若a2≠4b2,则a≠-2b | ||
| C. | 若a>-2b,则a2>4b2 | D. | 若a2=4b2,则a=-2b |
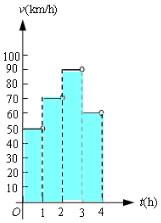 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示.