题目内容
13．已知tanα=2，求下列各式的值．（1）$\frac{sinα-4cosα}{5sinα+2cosα}$；
（2）sin2α+sin2α．
分析 （1）由条件利用同角三角函数的基本关系，求得要求式子的值．
（2）利用同角三角函数的基本关系，二倍角公式，求得要求式子的值．
解答 解：（1）∵tanα=2，∴$\frac{sinα-4cosα}{5sinα+2cosα}$=$\frac{tanα-4}{5tanα+2}$=-$\frac{1}{6}$；
（2）sin2α+sin2α=$\frac{{sin}^{2}α+2sinαcosα}{{sin}^{2}α{+cos}^{2}α}$=$\frac{{tan}^{2}α+2tanα}{{tan}^{2}α+1}$=$\frac{8}{5}$．
点评 本题主要考查同角三角函数的基本关系，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
18．已知定义在R上的函数f（x）满足：①f（x）=f（4-x），②f（x+2）=f（x），③在[0，1]上表达式为f（x）=2x-1，则函数g（x）=f（x）-log3|x|的零点个数为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
4．
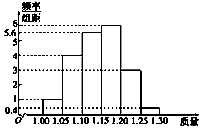为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．
（1）在下面表格中填写相应的频率；
（2）估计数据落在[1.15，1.30）中的概率为多少；
（3）将上面捕捞的100条鱼分别作一记号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．
为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．（1）在下面表格中填写相应的频率；
| 分组 | 频率 |
| [1.00，1.05） | |
| [1.05，1.10） | |
| [1.10，1.15） | |
| [1.15，1.20） | |
| [1.20，1.25） | |
| [1.25，1.30） |
（3）将上面捕捞的100条鱼分别作一记号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．