题目内容
14.若直线$\sqrt{3}x-2y=0$与圆(x-4)2+y2=r2(r>0)相切,则r=( )| A. | $\frac{48}{7}$ | B. | 5 | C. | $\frac{{4\sqrt{21}}}{7}$ | D. | 25 |
分析 由圆的方程求出圆心坐标,直接用圆心到直线的距离等于半径求得答案.
解答 解:由(x-4)2+y2=r2(r>0),可知圆心坐标为(1,0),半径为r,
∵直线$\sqrt{3}x-2y=0$与圆(x-4)2+y2=r2(r>0)相切,
由圆心到直线的距离d=$\frac{4\sqrt{3}}{\sqrt{3+4}}$=$\frac{4\sqrt{21}}{7}$,
可得圆的半径为$\frac{4\sqrt{21}}{7}$.
故选:C.
点评 本题考查了直线和圆的位置关系,考查了点到直线的距离公式的应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数图象的一个对称中心为( )
| A. | $(\frac{7π}{12},0)$ | B. | $(\frac{π}{6},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{2π}{3},-3)$ |
2.下列命题中正确的是( )
| A. | 两条直线都和同一个平面平行,则这两条直线平行 | |
| B. | 两条直线没有公共点,则这两条直线平行 | |
| C. | 两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 一条直线和一个平面内所有直线没有公共点,则这条直线和这个平面平行 |
19.圆${C_1}:{x^2}+{y^2}+2x+2y-2=0$与圆${C_2}:{x^2}+{y^2}-4x-2y+4=0$的公切线有( )
| A. | .1条 | B. | .2条 | C. | .3条 | D. | .4条 |
16.若直线l过点(-3,1)且被圆x2+y2=25截得的弦长为8,则直线l的方程是( )
| A. | x=-3或4x+3y-15=0 | B. | 4x-3y+15=0 | ||
| C. | 4x+3y-15=0 | D. | x=-3或4x-3y+15=0 |
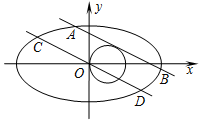 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.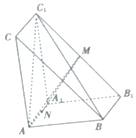 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点