题目内容
下列五个命题:
①函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-3,1].
②f(x)=|2-x|与f(x)=
表示相同函数;
③幂函数的图象都经过(0,0)和(1,1)点;
④一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1;
⑤函数f(x)定义在R上,若y=f(x+2)为偶函数,则y=f(x)的图象关于直线x=-2对称;
其中不正确的命题的序号是 .
①函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-3,1].
②f(x)=|2-x|与f(x)=
| x2-4x+4 |
③幂函数的图象都经过(0,0)和(1,1)点;
④一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1;
⑤函数f(x)定义在R上,若y=f(x+2)为偶函数,则y=f(x)的图象关于直线x=-2对称;
其中不正确的命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:对于①根据复合函数的定义域判断即可
对于②化简解析式直接证明即可
对于③举个反例即可
对于④画图即可
对于⑤根据函数图象的平移即可判断.
对于②化简解析式直接证明即可
对于③举个反例即可
对于④画图即可
对于⑤根据函数图象的平移即可判断.
解答:
解:对于①结论是不正确的,函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2].
对于②结论是正确的,f(x)=|2-x|=|x-2|,g(x)=
=
=|x-2|,故表示相同函数.
对于③结论是吧正确的,幂函数y=x-1不过(0,0)点.
对于④结论是正确的,如下图:m=0时有2个公共点,0<m<3时有4个公共点,m=3时有3个公共点,m>3时有2个公共点.

对于⑤是不正确的,y=f(x+2)为偶函数,则f(x+2)关于y轴对称,将f(x+2)向右平移2个单位得f(x),则
f(x)关于x=2对称.
故答案为:①③⑤
对于②结论是正确的,f(x)=|2-x|=|x-2|,g(x)=
| x2-4x+4 |
| (x-2)2 |
对于③结论是吧正确的,幂函数y=x-1不过(0,0)点.
对于④结论是正确的,如下图:m=0时有2个公共点,0<m<3时有4个公共点,m=3时有3个公共点,m>3时有2个公共点.

对于⑤是不正确的,y=f(x+2)为偶函数,则f(x+2)关于y轴对称,将f(x+2)向右平移2个单位得f(x),则
f(x)关于x=2对称.
故答案为:①③⑤
点评:本题以函数为载体考查了命题的概念,属于基础题.

练习册系列答案
相关题目
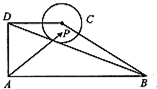 如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设
如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设