题目内容
20.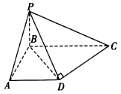 如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.(1)求证:平面PCD⊥平面PBD;
(2)求直线CD和平面PAD所成角的正弦值;
(3)在棱PA上是否存在一点E,使得平面PAB与平面BDE所成锐二面角的正切值为$\sqrt{5}$?若存在,指出点E的位置,若不存在,请说明理由.
分析 (1)推导出PB⊥CD,CD⊥PD,从而CD⊥平面PBD,由此能证明平面PCD⊥平面PBD.
(2)以B为原点,BA、BC、BP所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线CD和平面PAD所成角的正弦值.
(3)求出平面DEB的一个法向量和平面PAB的法向量,利用向量法能求出在棱PA上存在一点E,使得平面PAB与平面BDE所成锐二面角的正切值为$\sqrt{5}$,E为棱PA上靠近A的三等分点.
解答 证明:(1)∵PB⊥底面ABCD,∴PB⊥CD,
又∵CD⊥PD,PD∩PB=P,PD,PB?平面PBD,
∴CD⊥平面PBD,∵CD?平面PCD,
∴平面PCD⊥平面PBD.
解:(2)如图,以B为原点,BA、BC、BP所在直线分别为x,y,z轴,建立空间直角坐标系,
由(1)知△BCD是等腰直角三角形,∴BC=4,
设BP=b(b>0),则B(0,0,0),A(2,0,0),C(0,4,0),D(2,2,0),P(0,0,b),
则$\overrightarrow{PA}$=(2,0,-b),$\overrightarrow{CD}$=(2,-2,0),
∵异面直线PA、CD所成角为60°,
∴cos60°=$\frac{|\overrightarrow{PA}•\overrightarrow{CD}|}{|\overrightarrow{PA}|•|\overrightarrow{CD}|}$=$\frac{4}{\sqrt{4+{b}^{2}}•2\sqrt{2}}$=$\frac{1}{2}$,
解得b=2,
∵$\overrightarrow{AD}$=(0,2,0),$\overrightarrow{PA}$=(2,0,-2),
设平面PAD的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=2y=0}\\{\overrightarrow{n}•\overrightarrow{PA}=2x-2z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
设直线CD和平面PAD所成角为θ,
则sinθ=|cos<$\overrightarrow{CD},\overrightarrow{n}$>|=$\frac{|\overrightarrow{CD}•\overrightarrow{n}|}{|\overrightarrow{CD}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{2}•\sqrt{8}}$=$\frac{1}{2}$,
∴直线CD和平面PAD所成角的正弦值为$\frac{1}{2}$.
(3)假设棱PA上存在一点E,使得平面PAB与平面BDE所成锐二面角的正切值为$\sqrt{5}$,
设$\overrightarrow{PE}=λ\overrightarrow{PA}$,(0<λ<1),且E(x,y,z),则(x,y,z-2)=λ(2,0,-2),
∴E(2λ,0,2-2λ),设平面DEB的一个法向量为$\overrightarrow{m}$=(a,b,c),
$\overrightarrow{BE}$=(2λ,0,2-2λ),$\overrightarrow{BD}$=(2,2,0),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BE}=2λa+(2-2λ)c=0}\\{\overrightarrow{m}•\overrightarrow{BD}=2a+2b=0}\end{array}\right.$,取a=λ-1,得$\overrightarrow{m}$=(λ-1,λ-1,λ),
平面PAB的法向量$\overrightarrow{p}$=(0,1,0),
∵平面PAB与平面BDE所成锐二面角的正切值为$\sqrt{5}$,
∴平面PAB与平面BDE所成锐二面角的余弦值为$\frac{\sqrt{6}}{6}$,
∴|cos<$\overrightarrow{m},\overrightarrow{p}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{p}|}{|\overrightarrow{m}|•|\overrightarrow{p}|}$=$\frac{1-λ}{\sqrt{2(1-λ)^{2}+{λ}^{2}}}$=$\frac{\sqrt{6}}{6}$,
解得$λ=\frac{2}{3}$或λ=2(舍),
∴在棱PA上存在一点E,使得平面PAB与平面BDE所成锐二面角的正切值为$\sqrt{5}$,E为棱PA上靠近A的三等分点.
点评 本题考查面面垂直的证明,考查线面角的正弦值的求法,考查满足条件的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
 所得弦长为2,则圆心C的轨迹方程为( )
所得弦长为2,则圆心C的轨迹方程为( )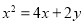 B.
B.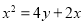
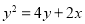 D.
D.
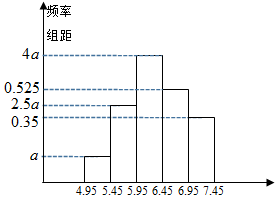 质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:
质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下: