题目内容
5.某次数学考试试题中共有10道选择题,每道选择题都有4个选项,其中仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分.”某考生每道题都给了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:(Ⅰ)得45分的概率;
(Ⅱ)所得分数ξ的数学期望.
分析 (Ⅰ)得分为45分,剩下4道必须再做对3道题,在其余的四道题中,有两道题答对的概率为$\frac{1}{2}$,有一道题答对的概率为$\frac{1}{3}$,还有一道答对的概率为$\frac{1}{4}$,由此能求出得分为45分的概率.
(Ⅱ)依题意,该考生得分的范围为{30,35,40,45,50},分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(Ⅰ)得分为45分,剩下4道必须再做对3道题,在其余的四道题中,
有两道题答对的概率为$\frac{1}{2}$,有一道题答对的概率为$\frac{1}{3}$,还有一道答对的概率为$\frac{1}{4}$,
所以得分为45分的概率为:
$P=\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{3}{4}+\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{4}+\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{4}=\frac{7}{48}$.
(Ⅱ)依题意,该考生得分的范围为{30,35,40,45,50}.
得分为30分表示只做对了6道题,其余各题都做错,所以概率为:${P_1}=\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{6}{48}=\frac{1}{8}$;
同理可以求得得分为35分的概率为:${P_2}=C_2^1×\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{3}{4}+\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{3}{4}+\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{1}{4}=\frac{17}{48}$;
得分为40)的概率为:${P_3}=\frac{17}{48}$;
得分为45)的概率为:${P_4}=\frac{7}{48}$;
得分为50)的概率为:${P_5}=\frac{1}{48}$.
可知ξ的分布列为:
| ξ | 30 | 35 | 40 | 45 | 50 |
| P | $\frac{6}{48}$ | $\frac{17}{48}$ | $\frac{17}{48}$ | $\frac{7}{48}$ | $\frac{1}{48}$ |
点评 本题考查考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查数据处理能力、运算求解能力,考查化归与转化思想、函数与方思想,是中档题.

| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
| A. | 12 | B. | 24 | C. | 16 | D. | 32 |
| A. | 320 | B. | 446 | C. | 482 | D. | 248 |
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
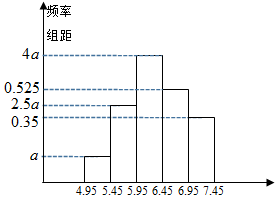 质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:
质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下: