题目内容
已知函数f(x)=x-1-alnx,a>0.
(Ⅰ)若对任意x∈(0,+∞),都有f(x)≥0恒成立,求实数a的取值集合;
(Ⅱ)证明:(1+
)n<e<(1+
)n+1(其中n∈N *,e为自然对数的底数).
(Ⅰ)若对任意x∈(0,+∞),都有f(x)≥0恒成立,求实数a的取值集合;
(Ⅱ)证明:(1+
| 1 |
| n |
| 1 |
| n |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知得x>0,f′(x)=1-
,利用导数性质求出f(x)极小值=f(a)=a-1-alna.由此求出a≥
.
(Ⅱ)设数列an=(1+
)n,数列bn=(1+
)n+1,由
(1+
)x=e,得:
an=e,
bn=e.由已知条件推导出数列{an}单调递增且数列{bn}单调递减,由此能证明(1+
)n<e<(1+
)n+1(其中n∈N *,e为自然对数的底数).
| a |
| x |
| 1 |
| 1-lna |
(Ⅱ)设数列an=(1+
| 1 |
| n |
| 1 |
| n |
| lim |
| x→∞ |
| 1 |
| x |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| n |
| 1 |
| n |
解答:
(Ⅰ)解:∵f(x)=x-1-alnx,a>0,
∴x>0,f′(x)=1-
,
由f′(x)=0,得x=a.
x∈(0,a)时,f′(x)<0;x∈(a,+∞)时,f′(x)>0.
∴f(x)的减区间是(0,a),增区间是(a,+∞),
∴f(x)极小值=f(a)=a-1-alna.
∵对任意x∈(0,+∞),都有f(x)≥0恒成立,
∴f(x)极小值=f(a)=a-1-alna≥0.
∴a≥
.
(Ⅱ)证明:设数列an=(1+
)n,数列bn=(1+
)n+1,
由
(1+
)x=e,得:
an=e,
bn=e.
因此只需证数列{an}单调递增且数列{bn}单调递减,
①证明数列{an}单调递增:
an=(1+
)n<(
)n+1
=(
)n+1=an+1,
∴数列{an}单调递增.
②证明数列{bn}单调递减:
bn=(1+
)n+1=
=
( 令 t=-(n+1),换元 )
=(1+
)t=at,
由①得at关于t单调递增,而t=-(n+1)关于n单调递减,
由复合函数的单调性知,{bn}.
∴(1+
)n<e<(1+
)n+1(其中n∈N *,e为自然对数的底数).
∴x>0,f′(x)=1-
| a |
| x |
由f′(x)=0,得x=a.
x∈(0,a)时,f′(x)<0;x∈(a,+∞)时,f′(x)>0.
∴f(x)的减区间是(0,a),增区间是(a,+∞),
∴f(x)极小值=f(a)=a-1-alna.
∵对任意x∈(0,+∞),都有f(x)≥0恒成立,
∴f(x)极小值=f(a)=a-1-alna≥0.
∴a≥
| 1 |
| 1-lna |
(Ⅱ)证明:设数列an=(1+
| 1 |
| n |
| 1 |
| n |
由
| lim |
| x→∞ |
| 1 |
| x |
| lim |
| n→∞ |
| lim |
| n→∞ |
因此只需证数列{an}单调递增且数列{bn}单调递减,
①证明数列{an}单调递增:
an=(1+
| 1 |
| n |
(1+
| ||||||
| n+1 |
=(
| n+2 |
| n+1 |
∴数列{an}单调递增.
②证明数列{bn}单调递减:
bn=(1+
| 1 |
| n |
| 1 | ||
(
|
=
| 1 | ||
(1-
|
=(1+
| 1 |
| t |
由①得at关于t单调递增,而t=-(n+1)关于n单调递减,
由复合函数的单调性知,{bn}.
∴(1+
| 1 |
| n |
| 1 |
| n |
点评:本题考查实数的取值范围的求法,考查不等式的证明,解题时要认真审题,注意构造成法、导数和极限性质的合理运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
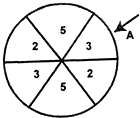 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).