题目内容
设集合A={x∈R|-1≤x≤1},B={x∈R|x(x-3)≤0},则A∩B等于( )
| A、{x∈R|-1≤x≤3} |
| B、{x∈R|0≤x≤3} |
| C、{x∈R|-1≤x≤0} |
| D、{x∈R|0≤x≤1} |
考点:交集及其运算
专题:集合
分析:求出集合B的元素,利用集合的基本运算即可得到结论.
解答:
解:B={x∈R|x(x-3)≤0}={x∈R|0≤x≤3},
则A∩B={x∈R|0≤x≤1},
故选:D.
则A∩B={x∈R|0≤x≤1},
故选:D.
点评:本题主要考查集合的基本运算,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若实数x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、-1 | B、2 | C、1 | D、0 |
△ABC外接圆半径等于1,其圆心O满足
=
(
+
),|
|=|
|,则向量
在
方向上的投影等于( )
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| AC |
| BA |
| BC |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知集合A={x|x2-2x<0},B={x|x≤-1或x>1},则A∩(∁RB)=( )
| A、{x|0<x<1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1<x<2} |
若x,y满足约束条件
,则函数z=2x-y的最大值是( )
|
| A、-1 | B、0 | C、3 | D、6 |
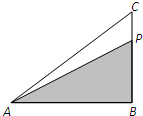 如图,在Rt△ABC中,AB=4,BC=3,点P在边BC上沿B→C运动,则△ABP的面积小于4的概率为
如图,在Rt△ABC中,AB=4,BC=3,点P在边BC上沿B→C运动,则△ABP的面积小于4的概率为