题目内容
已知直线l⊥平面α,直线m?平面β,有下列四个命题:
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β.
以上命题中,正确命题的序号是( )
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β.
以上命题中,正确命题的序号是( )
| A、①② | B、①③ | C、②④ | D、③④ |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用线面垂直、面面平行、面面垂直的性质定理和判定定理对四个命题分别分析解答.
解答:
解:已知直线l⊥平面α,直线m?平面β,
对于①,若α∥β,得到直线l⊥平面β,所以l⊥m;故①正确;
对于②,若α⊥β,直线l在β内或者l∥β,则l与m的位置关系不确定;
对于③,若l∥m,则直线m⊥α,由面面垂直的性质定理可得α⊥β;故③正确;
对于④,若l⊥m,则α与β可能相交;故④错误;
故选B.
对于①,若α∥β,得到直线l⊥平面β,所以l⊥m;故①正确;
对于②,若α⊥β,直线l在β内或者l∥β,则l与m的位置关系不确定;
对于③,若l∥m,则直线m⊥α,由面面垂直的性质定理可得α⊥β;故③正确;
对于④,若l⊥m,则α与β可能相交;故④错误;
故选B.
点评:本题考查了线面垂直、面面平行、面面垂直的性质定理和判定定理的运用,熟练掌握定理的题设和结论是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中,在(0,+∞)上为减函数的是( )
| A、y=log2(x+1) | ||
B、y=-
| ||
C、y=
| ||
D、y=(
|
已知变量x,y,满足约束条件
,则z=3x+y的最大值为( )
|
| A、3 | ||
| B、12 | ||
C、
| ||
| D、10 |
直角坐标系中,y=ax+
与y=ax2的图象可能是( )
| 1 |
| a |
A、 |
B、 |
C、 |
D、 |
 给出的是计算
给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |
| A、I<=100 |
| B、I>100 |
| C、I>50 |
| D、I<=50 |
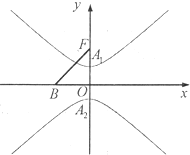 已知点A1,A2是双曲线
已知点A1,A2是双曲线| y2 |
| a2 |
| x2 |
| b2 |
A、(1,
| ||||||
B、(1,
| ||||||
C、(
| ||||||
D、(
|