题目内容

18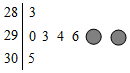．2016年2月，某品牌汽车对某地区的八家4S店该月的销售量进行了统计，统计数据如茎叶图所示，由于工作人员失误不慎丢掉两个数据，已知这些数据的平均数与方差分别为293与33.5，则残缺的两个数字中较小的数字为1．

分析 设残缺的两个数字中较小的数字为x，另一个为y，根据平均数与方差的概念列出方程组，结合茎叶图的特征，即可求出x、y的值．

解答 解：设残缺的两个数字中较小的数字为x，另一个为y，则
$\frac{1}{8}$×（283+290+293+294+296+290+290+x+y+305）=293①，
$\frac{1}{8}$×[（293-283）2+（293-290）2+（293-293）2+（294-293）2+（296-293）2
+（290+x-293）2+（290+y-293）2+（305-293）2]=33.5②；
化简①得，x+y=3③；
化简②得，（x-3）2+（y-3）2=5④；
又x、y∈N，且x＜y；
∴x=1，y=2；
即残缺的两个数字中较小的数字为1．
故答案为：1．

点评 本题利用茎叶图考查了平均数与方差的应用问题，是基础题目．

练习册系列答案
相关题目
8．已知函数$f（x）=\sqrt{3}sinxcosx+{sin^2}x-\frac{1}{2}$．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求f（x）在区间$[\frac{π}{4}，\frac{π}{2}]$上的最大值和最小值．
9．已知△ABC的内角为A、B、C，其对边分别为a、b、c，已知B为锐角，向量$\overrightarrow m=（2sinB，-\sqrt{3}），\overrightarrow n=（cos2B，2{cos^2}\frac{B}{2}-1）$，且$\overrightarrow m$∥$\overrightarrow n$．
（Ⅰ）求角B的大小及当$b∈[\sqrt{3}，2\sqrt{3}]$时，△ABC的外接圆半径R的取值范围；
（Ⅱ）如果b=2，求S△ABC的最大值．
6．一辆赛车在一个周长为3km的封闭跑道上行驶，跑道由几段直道和弯道组成，图1反应了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系．

根据图1，有以下四个说法：
①在这第二圈的2.6km到2.8km之间，赛车速度逐渐增加；
②在整个跑道上，最长的直线路程不超过0.6km；
③大约在这第二圈的0.4km到0.6km之间，赛车开始了那段最长直线路程的行驶；
④在图2的四条曲线（注：s为初始记录数据位置）中，曲线B最能符合赛车的运动轨迹．
其中，所有正确说法的序号是①④．
13．已知复数z满足$（1-i）\overline z=5+i$，则z=（　　）
A．2+3iB．2-3iC．3+2iD．3-2i
3．已知|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，$\overrightarrow a$与$\overrightarrow b$的夹角为120°，$\overrightarrow c$=$\overrightarrow a$+2$\overrightarrow b$，$\overrightarrow d$=2$\overrightarrow a$+k$\overrightarrow b$，当实数k取何值时：
（1）$\overrightarrow c⊥\overrightarrow d$．
（2）$\overrightarrow c∥\overrightarrow d$．
10．证明下列各式：
（1）sin4α-cos4α=sin2α-cos2α；
（2）sin2α•cos2α+sin2α+cos4α=1．
7．设函数f（x）=asinωx+bcosωx+1（ab≠0，ω＞0）的周期为π，f（x）有最大值4，且f（$\frac{π}{6}$）=$\frac{3\sqrt{3}}{2}$+1，求a、b的值．
10．若函数f（x）=$\frac{lnx}{1+x}$-lnx在x=x0处取得最大值，则下列结论正确的是（　　）
A．f（x0）＜x0B．f（x0）=x0C．f（x0）＞x0D．f（x0）=-x0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网