题目内容
8.已知函数$f(x)=\sqrt{3}sinxcosx+{sin^2}x-\frac{1}{2}$.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求f(x)在区间$[\frac{π}{4},\frac{π}{2}]$上的最大值和最小值.
分析 (Ⅰ)化简f(x),从而求出周期T;(Ⅱ)根据x的范围,求出2x-$\frac{π}{6}$的范围,从而求出f(x)的最大值和最小值即可.
解答 解:$f(x)=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x$=$sin(2x-\frac{π}{6})$,
(Ⅰ)$T=\frac{2π}{2}=π$;
(Ⅱ)∵$\frac{π}{4}≤x≤\frac{π}{2}$,∴$\frac{π}{3}≤2x-\frac{π}{6}≤\frac{5π}{6}$,
即$\frac{1}{2}≤sin(2x-\frac{π}{6})≤1$,
由此得到:f(x)max=1,此时$x=\frac{π}{3}$;
∴$f{(x)_{min}}=\frac{1}{2}$,此时$x=\frac{π}{2}$.
点评 本题考查了三角函数变换问题,考查求函数的周期以及函数的值域问题,是一道中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
3.已知函数f(x)的导函数f′(x)=2+sinx,且f(0)=-1,数列{an}是以$\frac{π}{4}$为公差的等差数列,若f(a2)+f(a3)+f(a4)=3π,则$\frac{{a}_{2016}}{{a}_{2}}$=( )
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
13.复数z=$\frac{3+i}{1-i}$(其中i为虚数单位)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
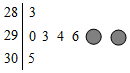 2016年2月,某品牌汽车对某地区的八家4S店该月的销售量进行了统计,统计数据如茎叶图所示,由于工作人员失误不慎丢掉两个数据,已知这些数据的平均数与方差分别为293与33.5,则残缺的两个数字中较小的数字为1.
2016年2月,某品牌汽车对某地区的八家4S店该月的销售量进行了统计,统计数据如茎叶图所示,由于工作人员失误不慎丢掉两个数据,已知这些数据的平均数与方差分别为293与33.5,则残缺的两个数字中较小的数字为1.