题目内容
3.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow a$与$\overrightarrow b$的夹角为120°,$\overrightarrow c$=$\overrightarrow a$+2$\overrightarrow b$,$\overrightarrow d$=2$\overrightarrow a$+k$\overrightarrow b$,当实数k取何值时:(1)$\overrightarrow c⊥\overrightarrow d$.
(2)$\overrightarrow c∥\overrightarrow d$.
分析 (1)可先由条件得出$\overrightarrow{a}•\overrightarrow{b}=-6$,而$\overrightarrow{c}⊥\overrightarrow{d}$时,$\overrightarrow{c}•\overrightarrow{d}=0$,从而可得到32-6(4+k)+18k=0,这样即可求出k的值;
(2)根据条件可知$\overrightarrow{c},\overrightarrow{d}$不共线,从而由$\overrightarrow{c}∥\overrightarrow{d}$可得$\overrightarrow{d}=x\overrightarrow{c}$,即得到$2\overrightarrow{a}+k\overrightarrow{b}=x\overrightarrow{a}+2x\overrightarrow{b}$,从而由平面向量基本定理即可得到关于k,x的方程组,解方程组即可得出k的值.
解答 解:根据条件,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°=-6$;
(1)若$\overrightarrow{c}⊥\overrightarrow{d}$,则$\overrightarrow{c}•\overrightarrow{d}=0$;
即$(\overrightarrow{a}+2\overrightarrow{b})•(2\overrightarrow{a}+k\overrightarrow{b})=2{\overrightarrow{a}}^{2}+(4+k)\overrightarrow{a}•\overrightarrow{b}+2k{\overrightarrow{b}}^{2}$=32-6(4+k)+18k=0;
∴$k=-\frac{2}{3}$;
即$k=-\frac{2}{3}$时,$\overrightarrow{c}⊥\overrightarrow{d}$;
(2)若$\overrightarrow{c}∥\overrightarrow{d}$,根据题意知,$\overrightarrow{c},\overrightarrow{d}$都为非零向量且不共线;
∴存在x,使$\overrightarrow{d}=x\overrightarrow{c}$;
即$2\overrightarrow{a}+k\overrightarrow{b}=x\overrightarrow{a}+2x\overrightarrow{b}$;
∴由平面向量基本定理得$\left\{\begin{array}{l}{x=2}\\{2x=k}\end{array}\right.$;
∴k=4;
即k=4时,$\overrightarrow{c}∥\overrightarrow{d}$.
点评 考查向量数量积的运算及计算公式,向量垂直的充要条件,以及平面向量和共线向量基本定理.

 应用题作业本系列答案
应用题作业本系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
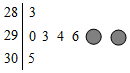 2016年2月,某品牌汽车对某地区的八家4S店该月的销售量进行了统计,统计数据如茎叶图所示,由于工作人员失误不慎丢掉两个数据,已知这些数据的平均数与方差分别为293与33.5,则残缺的两个数字中较小的数字为1.
2016年2月,某品牌汽车对某地区的八家4S店该月的销售量进行了统计,统计数据如茎叶图所示,由于工作人员失误不慎丢掉两个数据,已知这些数据的平均数与方差分别为293与33.5,则残缺的两个数字中较小的数字为1.