题目内容
7.设函数f(x)=asinωx+bcosωx+1(ab≠0,ω>0)的周期为π,f(x)有最大值4,且f($\frac{π}{6}$)=$\frac{3\sqrt{3}}{2}$+1,求a、b的值.分析 由题意结合周期性可得ω,进而由最值和已知式子可得ab的方程组,解方程组验证即可.
解答 解:∵函数f(x)=asinωx+bcosωx+1的周期为π,f(x)有最大值4,
∴$\frac{2π}{ω}$=π且$\sqrt{{a}^{2}+{b}^{2}}$+1=4,解得ω=2,a2+b2=9,①
又∵f($\frac{π}{6}$)=$\frac{3\sqrt{3}}{2}$+1,∴asin$\frac{π}{3}$+bcos$\frac{π}{3}$+1
=$\frac{\sqrt{3}}{2}$a+$\frac{1}{2}$b+1=$\frac{3\sqrt{3}}{2}$+1,∴$\frac{\sqrt{3}}{2}$a+$\frac{1}{2}$b=$\frac{3\sqrt{3}}{2}$,②
联立①②可解得$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=\frac{3\sqrt{3}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=0}\end{array}\right.$,
由ab≠0可知a、b的值分别为$\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和最值以及方程组的解法,属中档题.

练习册系列答案
相关题目
16.已知sinα•cosβ=1,那么sin(α+β)等于( )
| A. | 0 | B. | -1 | C. | ±1 | D. | 1 |
19.f(x)是定义在(0,+∞)上单调函数,且对?x∈(0,+∞),都有f(f(x)-lnx)=e+1,则方程f(x)-f′(x)=e的实数解所在的区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,e) | D. | (e,3) |
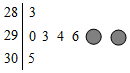 2016年2月,某品牌汽车对某地区的八家4S店该月的销售量进行了统计,统计数据如茎叶图所示,由于工作人员失误不慎丢掉两个数据,已知这些数据的平均数与方差分别为293与33.5,则残缺的两个数字中较小的数字为1.
2016年2月,某品牌汽车对某地区的八家4S店该月的销售量进行了统计,统计数据如茎叶图所示,由于工作人员失误不慎丢掉两个数据,已知这些数据的平均数与方差分别为293与33.5,则残缺的两个数字中较小的数字为1.