题目内容
已知函数f(x)=x+
.
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在[-1,0)上是否有最大值和最小值?如果有最大值或最小值,请求出最值.
| 1 |
| x |
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在[-1,0)上是否有最大值和最小值?如果有最大值或最小值,请求出最值.
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:(I)用函数奇偶性定义证明,要注意定义域.(II)先任取两个变量,且界定大小,再作差变形看符号,(III)由函数图象判断即可.
解答:
解:(Ⅰ)证明:(I)函数为奇函数f(-x)=-x-
=-f(x),
(II)设x1,x2∈(0,1)且x1<x2,
f(x2)-f(x1)=x2+
-x1-
=
,
∵0<x1<x2<1,∴x1x2<1,x1x2-1<0,
∵x2>x1∴x2-x1>0.
∴f(x2)-f(x1)<0,f(x2)<f(x1),
因此函数f(x)在(0,1)上是减函数,
(III)由(Ⅰ)(Ⅱ)得:
f(x)在[-1,0)上是减函数,
∴f(x)max=f(-1)=-2,无最小值.
| 1 |
| x |
(II)设x1,x2∈(0,1)且x1<x2,
f(x2)-f(x1)=x2+
| 1 |
| x2 |
| 1 |
| x1 |
| (x2-x1)(x1x2-1) |
| x1x2 |
∵0<x1<x2<1,∴x1x2<1,x1x2-1<0,
∵x2>x1∴x2-x1>0.
∴f(x2)-f(x1)<0,f(x2)<f(x1),
因此函数f(x)在(0,1)上是减函数,
(III)由(Ⅰ)(Ⅱ)得:
f(x)在[-1,0)上是减函数,
∴f(x)max=f(-1)=-2,无最小值.
点评:本题主要考查函数奇偶性和单调性定义,要注意奇偶性要先判断,单调性变形要到位.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
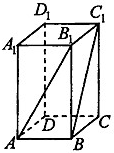 如图,在长方体ABCD-A1B1C1D1中,AB=
如图,在长方体ABCD-A1B1C1D1中,AB=| 2 |
| 3 |
| 6 |
| A、60° | B、45° |
| C、30° | D、15° |
若函数f(x)对任意a>0且a≠1,都有f(ax)=af(x),则称函数为“穿透”函数,则下列函数中,不是“穿透”函数的是( )
| A、f(x)=-x |
| B、f(x)=x+1 |
| C、f(x)=|x| |
| D、f(x)=x-|x| |
平面α的斜线l与它在这个平面上射影l′的方向向量分别为
=(1,0,1),
=(0,1,1),则斜线l与平面α所成的角为( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |