题目内容
8.已知函数f(x)=$\sqrt{3}({sin^2}x-{cos^2}x)+2sinxcosx$.(1)求f(x)最小正周期;
(2)设$x∈[-\frac{π}{3},\;\frac{π}{3}]$,求f(x)的值域和单调递增区间.
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,求得f(x)最小正周期.
(2)由条件利用正弦函数的定义域和值域,求得f(x)的值域,再利用正弦函数的单调性,求得f(x)的增区间.
解答 解:(1)∵函数f(x)=$\sqrt{3}({sin^2}x-{cos^2}x)+2sinxcosx$=-$\sqrt{3}$cos2x+sin2x=2sin(2x-$\frac{π}{3}$),
∴f(x)最小正周期为$\frac{2π}{2}$=π.
(2)设$x∈[-\frac{π}{3},\;\frac{π}{3}]$,则2x-$\frac{π}{3}$∈[-π,$\frac{π}{3}$],∴sin(2x-$\frac{π}{3}$)∈[-1,$\frac{\sqrt{3}}{2}$],
∴求f(x)的值域为[-2,$\sqrt{3}$].
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$],故函数的增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的周期性、定义域和值域、单调性,属于中档题.

练习册系列答案
相关题目
4.cos1050°=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
3.设集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0},若A∩B中恰有一个整数,则实数a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | [$\frac{3}{4}$,$\frac{4}{3}$) | C. | $[\frac{3}{4},+∞)$ | D. | (1,+∞) |
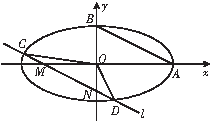 如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.
如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.