题目内容
3.已知数列{an}的前n项和为Sn,a1=1,an≠0,anan+1=4Sn-1(n∈N*)则数列{an}的通项公式为an=2n-1.分析 由anan+1=4Sn-1,可得当n≥2时,an-1an=4Sn-1-1,an≠0,两式相减化为an+1-an-1=4,可得数列{an}的奇数项与偶数项分别为等差数列,进而得出数列{an}的通项公式.
解答 解:∵anan+1=4Sn-1,
∴当n≥2时,an-1an=4Sn-1-1,anan+1-an-1an+1=4an,
∵an≠0,∴an+1-an-1=4,
当n=1时,a1a2=4a1-1,a1=1,解得a2=3,
∴数列{an}的奇数项与偶数项分别为等差数列,公差为4,首项分别为1,3.
∴当n=2k-1(k∈N*)为奇数时,an=a2k-1=1+4(k-1)=4k-3=2n-1;
当n=2k(k∈N*)为偶数时,an=a2k=3+4(k-1)=2n-1.
可得an=2n-1.
故答案为:an=2n-1.
点评 本题考查了递推式的应用、等差数列的定义及其通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
13.函数f(x)=lnx+1的定义域为( )
| A. | (0,+∞) | B. | (1,+∞) | C. | (-1,+∞) | D. | R |
14.已知如图所示的程序框图,当输入n=99时,输出S的值( )
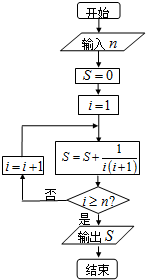

| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |
18.仔细观察下面○和●的排列规律:○●○○●○○○●○○○○●○○○○○●○○○○○○●…
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
8.如图是-个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为( )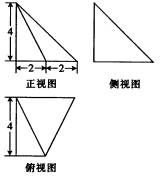

| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |