题目内容
2.已知△ABC满足A=$\frac{π}{3}$,($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{BC}$=0,点M在△ABC外,且MB=2MC=2,则MA的取值范围是[1,3].分析 由题意可知,△ABC为等边三角形,再结合题意画出图形,分M与A在BC同侧及M与A在BC异侧两种情况,利用正弦定理和余弦定理结合求得MA的取值范围,最后取并集得答案.
解答  解:由△ABC满足A=$\frac{π}{3}$,($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{BC}$=0,
解:由△ABC满足A=$\frac{π}{3}$,($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{BC}$=0,
可得△ABC为等边三角形,
又点M在△ABC外,且MB=2MC=2,
如图1.若M与A在BC同侧,
设∠BMC=β,∠BCM=α,
则$\frac{a}{sinβ}=\frac{2}{sinα}=\frac{1}{sin(α+β)}$,
可得1-2cosβ=a•cosα,
又cosα=$\frac{{a}^{2}-3}{2a}$,
∴|MA|2=a2+1-2acos(α-60°)=5-4cos(β-60°)∈[1,7),
则|MA|∈[1,$\sqrt{7}$);
如图2.若M与A在BC异侧,
设∠BMC=β,∠BCM=α,
则$\frac{a}{sinβ}=\frac{2}{sinα}=\frac{1}{sin(α+β)}$,
可得1-2cosβ=a•cosα,
又cosα=$\frac{{a}^{2}-3}{2a}$,
∴|MA|2=a2+1-2a•cos(α+60°)=5+4sin(β-60°)∈($5-2\sqrt{3}$,9],
则|MA|∈($\sqrt{5-2\sqrt{3}}$,3].
综上,|MA|的最小值为1,最大值为3,
故答案为:[1,3].
点评 本题考查平面向量的数量积运算,考查了三角形的解法,体现了分类讨论的数学思想方法,灵活转化是解决该题的关键,题目设置难度较大.

练习册系列答案
相关题目
17.已知复数$z=\frac{1-i}{2-i}$(其中i为虚数单位),则复数z在坐标平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.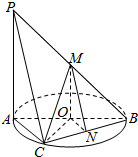 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
①OC∩平面PAC;②MO∥平面PAC;③平面PAC∥平面MON,
其中正确的命题是( )
 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:①OC∩平面PAC;②MO∥平面PAC;③平面PAC∥平面MON,
其中正确的命题是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
14.已知区间D⊆[0,2π],函数y=cosx在区间D上是增函数,函数y=sinx在区间D上是减函数,那么区间D可以是( )
| A. | [0,$\frac{π}{2}$] | B. | [$\frac{π}{2}$,π] | C. | [π,$\frac{3π}{2}$] | D. | [$\frac{3π}{2}$,2π] |