题目内容
4.已知函数f(x)=$\frac{{x}^{2}+2x+1}{x}$,其中x∈[1,+∞).(1)判断f(x)的单调性并证明;
(2)求f(x)的最小值.
分析 (1)可判断f(x)在[1,+∞)上是增函数,利用导数证明即可.
(2)由f(x)在[1,+∞)上是增函数知在x=1处有最小值.
解答 解:(1)f(x)=$\frac{{x}^{2}+2x+1}{x}$=x+$\frac{1}{x}$+2,
故f(x)在[1,+∞)上是增函数,证明如下,
∵f(x)=x+$\frac{1}{x}$+2,
∴f′(x)=1-$\frac{1}{{x}^{2}}$≥0,
故f(x)在[1,+∞)上是增函数;
(2)∵f(x)在[1,+∞)上是增函数,
∴fmin(x)=f(1)=1=1+2=4.
点评 本题考查了函数的单调性的判断与应用,同时考查了导数的应用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
14.在空间中,设l,m为两条不同直线,α,β为两个不同的平面,则下列命题正确的是( )
| A. | 若l?α,m不平行于l,则m不平行于α | |
| B. | 若l?α,m?β,且α,β不平行,则l,m不平行 | |
| C. | 若l?α,m不垂直于l,则m不垂直于α | |
| D. | 若l?α,m?β,l不垂直于m,则α,β不垂直 |
19.已知曲线y=f(x)在点(x0,y0)处的导数为f′(x0),若该曲线在点(x0,y0)处切线的斜率为2,则( )
| A. | x0=2 | B. | f(x0)=2 | C. | f′(x0)=2 | D. | $\frac{{y}_{0}}{{x}_{0}}$=2 |
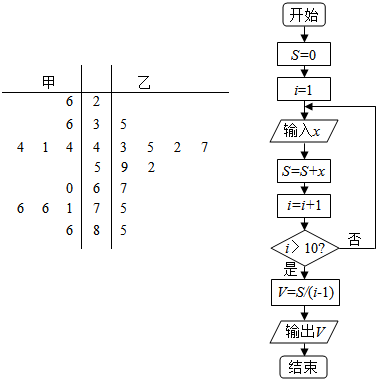 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.