题目内容
14.已知函数f(x)是奇函数,当x∈[-1,0]时,f(x)=$\frac{1}{{4}^{x}}$-$\frac{1}{{2}^{x}}$,则当x∈(0,1]时,f(x)=-4x+2x.分析 要设x∈(0,1],则-x∈[-1,0]根据,当x∈[-1,0]时,f(x)=$\frac{1}{{4}^{x}}$-$\frac{1}{{2}^{x}}$,可得f(-x)=$\frac{1}{{4}^{-x}}$-$\frac{1}{{2}^{-x}}$,利用f(-x)=-f(x)可求当x∈(0,1]时,f(x)的解析式.
解答 解:设x∈(0,1],则-x∈[-1,0]
∵当x∈[-1,0]时,f(x)=$\frac{1}{{4}^{x}}$-$\frac{1}{{2}^{x}}$,
∴f(-x)=$\frac{1}{{4}^{-x}}$-$\frac{1}{{2}^{-x}}$
由函数f(x)为奇函数可得f(-x)=-f(x)
∴f(x)=-f(-x)=-4x+2x,
故答案为:-4x+2x.
点评 本题主要考查了利用函数的奇偶性求解函数的解析式,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.过点M(-2,a),N(a,4)的直线的斜率为-$\frac{1}{2}$,则|MN|=( )
| A. | 10 | B. | 180 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{5}$ |
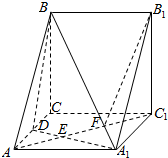 三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.
三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.