题目内容
12.在△ABC中,AH交BC于H,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AH}$,若$\overrightarrow{AM}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$,则λ+μ=$\frac{1}{3}$.分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AH}$,由B,H,C三点共线得出结论.
解答  解:$\overrightarrow{AH}=3\overrightarrow{AM}$=3λ$\overrightarrow{AB}$+3μ$\overrightarrow{AC}$.∵B,H,C三点共线,∴3λ+3μ=1,∴λ+μ=$\frac{1}{3}$.
解:$\overrightarrow{AH}=3\overrightarrow{AM}$=3λ$\overrightarrow{AB}$+3μ$\overrightarrow{AC}$.∵B,H,C三点共线,∴3λ+3μ=1,∴λ+μ=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了平面向量的基本定理及其应用,B,H,C三点共线是解题关键.

练习册系列答案
相关题目
2.下列数列中,构成等比数列的是( )
| A. | 2,3,4,5 | B. | 1,-2,-4,8 | C. | 0,1,2,4 | D. | 16,-8,4,-2 |
3.阅读如图所示的程序框图,运行相应的程序,输出的结果为( )


| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
7.若双曲线2kx2-ky2=1的一个焦点的坐标为(0,4),则k的值为( )
| A. | $\frac{3}{32}$ | B. | $\frac{16}{3}$ | C. | -$\frac{3}{32}$ | D. | -$\frac{16}{3}$ |
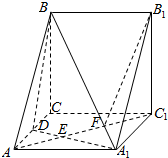 三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.
三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.