题目内容
已知F是抛物线y2=4x的焦点，直线l与抛物线相交于A，B两点，线段AB的中点M（
，3），则直线l的斜率是 ．
| 5 |
| 2 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设点作差，利用线段AB的中点坐标，即可求出直线l的斜率．
解答：
解：
，则
∵A，B在曲线上，∴
=4x1，
=4x2，
两式相减可得（y1+y2）（y1-y2）=4（x1-x2），
∵线段AB的中点M（
，3），
∴6（y1-y2）=4（x1-x2），
∴
=
．
故答案为：
．
|
∵A，B在曲线上，∴
| y | 2 1 |
| y | 2 2 |
两式相减可得（y1+y2）（y1-y2）=4（x1-x2），
∵线段AB的中点M（
| 5 |
| 2 |
∴6（y1-y2）=4（x1-x2），
∴
| y1-y2 |
| x1-x2 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查点差法，考查直线的斜率，考查学生的计算能力，属于基础题．
练习册系列答案
天天向上口算本系列答案
相关题目
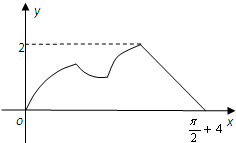
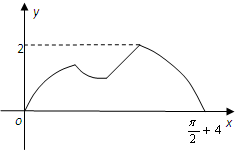
已知函数f（x）=2sin（ωx+φ）（其中x∈R，ω＞0，-π＜φ＜π）的部分图象如图所示．如果对函数g（x）的图象进行如下变化：横坐标扩大为原来的2倍，纵坐标不变，也可得到f（x）函数的图象，则函数g（x）的解析式是
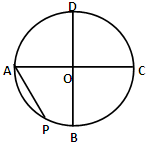如图，圆O的半径为1，AC⊥BD，动点P从点A出发，沿圆弧
