Question

20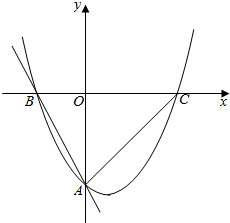．如图，抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A，交x轴于点B，抛物线与x轴的另一个交点为C，O为坐标原点
（1）求抛物线的解析式；
（2）抛物线上是否存在点P，使A，B，C，P四点构成平行四边形？存在，请求出P点坐标；若不存在，请说明理由；（3）若点M在y轴上，且∠ACB=∠OAB+∠OMB，请求出M点坐标．

Answer 1

分析 （1）求出A，B坐标，代入抛物线方程解出b，c；
（2）假设存在符合条件的P点，根据平行四边形的性质列出方程看是否有解；
（3）利用差角的正切公式计算出∠OMB的正切，结合正切的定义求出OM，得出M坐标．

解答 解：（1）∵直线y=-2x-4交y轴于点A，交x轴于点B，∴A（0，-4），B（-2，0），
把A（0，-4），B（-2，0）代入抛物线方程得$\left\{\begin{array}{l}{c=-4}\\{2-2b+c=0}\end{array}\right.$，解得b=-1，c=-4．
∴抛物线的解析式是y=$\frac{1}{2}$x²-x-4．
（2）令y=$\frac{1}{2}$x²-x-4=0解得x=-2或x=4，∴C（4，0）．
假设抛物线上存在点P使得A，B，C，P四点构成平行四边形，
①若BC是平行四边形的对角线，则AP的中点为BC的中点（1，0）．
设P（x，$\frac{1}{2}$x²-x-4），则$\left\{\begin{array}{l}{x=2}\\{\frac{1}{2}{x}^{2}-x-4=4}\end{array}\right.$，方程组无解．
②若BC是平行四边形的一边，则AP∥BC，且AP=BC，
由图象可知上述条件显然不成立，
综上，抛物线上不存在点P使得A，B，C，P四点构成平行四边形．
（3）∵tan∠ACB=$\frac{|OC|}{|OA|}$=1，tan∠OAB=$\frac{|OB|}{|OC|}$=$\frac{1}{2}$．∴tan∠OMB=$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$．
∵tan∠OMB=$\frac{|OB|}{|OM|}$=$\frac{2}{|OM|}$，∴|OM|=6．∴M（0，6）或M（0，-6）．

点评 本题考查了待定系数法求解析式，平行四边形的性质，三角函数计算，属于中档题．