题目内容
6.定义在R上的函数f(x)=$\left\{\begin{array}{l}{\frac{1}{2}(x=0)}\\{lg|x|(x≠0)}\end{array}\right.$,若关于x的方程f2(x)+bf(x)+c=0恰有三个不同的实数解x1,x2,x3,则x12+x22+x32=20.分析 设t=f(x),作出函数f(x)的图象,根据关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解x1,x2,x3,得到t的取值情况即可求出结论.
解答 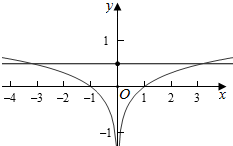 解:设t=f(x),则关于x的方程f2(x)+bf(x)+c=0等价为t2+bt+c=0,
解:设t=f(x),则关于x的方程f2(x)+bf(x)+c=0等价为t2+bt+c=0,
作出f(x)的图象如图:
由图象可知当t=$\frac{1}{2}$时,方程f(x)=$\frac{1}{2}$有三个根,当t≠$\frac{1}{2}$时方程f(x)=t有两个不同的实根,
∴若关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解x1,x2,x3,
则等价为t2+bt+c=0只有一个根t=$\frac{1}{2}$,
由f(x)=$\frac{1}{2}$得,x=0,或者lg|x|=$\frac{1}{2}$,
即得x=±10${\;}^{\frac{1}{2}}$=±$\sqrt{10}$,
即三个根x1,x2,x3,分别为0,$\sqrt{10}$或-$\sqrt{10}$,
∴x12+x22+x32═0+10+10=20.
故答案为:20.
点评 本题主要考查方程根的个数的应用,利用换元法将方程转化为二次方程,根据二次方程根的分布是解决本题的关键,利用数形结合是解决本题的基本思想.

练习册系列答案
相关题目
17.设命题p:?n∈N,n2>2n,则¬p为( )
| A. | ?n∈N,n2≤2n | B. | ?n∈N,n2<2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2<2n |
11.已知圆O1:x2+y2-4x+4y-41=0,圆O2:(x+1)2+(y-2)2=4,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
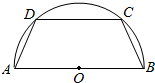 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.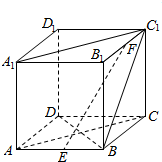 已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.
已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.