题目内容
4.已知$\overrightarrow{a}=(-3,2,5)$,$\overrightarrow{b}=(1,m,3)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则常数m=( )| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
分析 根据$\overrightarrow{a}⊥\overrightarrow{b}$时,$\overrightarrow{a}$•$\overrightarrow{b}$=0,列出方程求出m的值.
解答 解:$\overrightarrow{a}=(-3,2,5)$,$\overrightarrow{b}=(1,m,3)$,
当$\overrightarrow{a}⊥\overrightarrow{b}$时,$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即-3×1+2m+5×3=0,
解得m=-6.
故选:A.
点评 本题考查了空间向量的数量积的应用问题,是基础题目.

练习册系列答案
相关题目
19.某工厂对某种产品的产量与成本的资料分析后有如下数据:
经过分析,知道产量x和成本y之间具有线性相关关系.
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)试根据(1)求出的线性回归方程,预测产量为10千件时的成本.
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)试根据(1)求出的线性回归方程,预测产量为10千件时的成本.
16.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{2-lo{g}_{2}x,x>2}\end{array}\right.$若a,b,c互不相等,且f(a)=f(b)=f(c),则ab+bc+ca的取值范围是( )
| A. | (1,4) | B. | (2,4) | C. | (6,9) | D. | (7,9) |
14.已知p:x2-2x-3<0,q:x+2≥0,则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
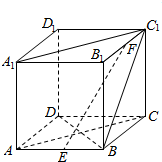 已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.
已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.