题目内容
已知动点P到点F(2,0)的距离与到直线l:x=
的距离之比为2.
(1)求点P的轨迹C的方程;
(2)直线l的方程为x+y-2=0,l与曲线C交于A,B两点.求线段AB的长.
| 1 |
| 2 |
(1)求点P的轨迹C的方程;
(2)直线l的方程为x+y-2=0,l与曲线C交于A,B两点.求线段AB的长.
考点:轨迹方程,直线与圆的位置关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设P(x,y),利用动点P到点F(2,0)的距离与到直线l:x=
的距离之比为2,建立方程,化简可得结论;
(2)直线l的方程与轨迹C的方程联立,消去y,利用韦达定理,结合弦长公式,可求线段AB的长.
| 1 |
| 2 |
(2)直线l的方程与轨迹C的方程联立,消去y,利用韦达定理,结合弦长公式,可求线段AB的长.
解答:
解:(1)设P(x,y),则
∵动点P到点F(2,0)的距离与到直线l:x=
的距离之比为2,
∴
=2,
化简可得x2-
=1;
(2)设交点A,B的坐标分别为A(x1,y1),B(x2,y2),
直线l的方程与轨迹C的方程联立,消去y可得2x2+4x-7=0,
∴x1+x2=-2,x1x2=-
,
∴|x1-x2|2=(x1+x2)2-4x1x2=18,
∴|x1-x2|=3
,
∴|AB|=
•|x1-x2|=6.
∵动点P到点F(2,0)的距离与到直线l:x=
| 1 |
| 2 |
∴
| ||
|x-
|
化简可得x2-
| y2 |
| 3 |
(2)设交点A,B的坐标分别为A(x1,y1),B(x2,y2),
直线l的方程与轨迹C的方程联立,消去y可得2x2+4x-7=0,
∴x1+x2=-2,x1x2=-
| 7 |
| 2 |
∴|x1-x2|2=(x1+x2)2-4x1x2=18,
∴|x1-x2|=3
| 2 |
∴|AB|=
| 2 |
点评:本题考查轨迹方程,考查直线与双曲线的位置关系,考查弦长的计算,正确求出双曲线的方程是关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知方程组
对此方程组的每一组正实数解(x,y,z,u),其中z≥y,都存在正实数M,且满足M≤
,则M的最大值是( )
|
| z |
| y |
| A、1 | ||
B、3+2
| ||
C、6+4
| ||
D、3-2
|
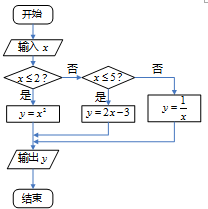 给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
给出了一个程序框图,其作用是输入x的值,输出相应的y的值,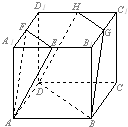 如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,
如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点, 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2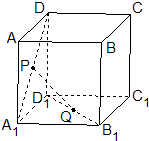 正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.
正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.