题目内容
设函数f(x)=|x2-1|+x2+kx.
(1)若k=2,求方程f(x)=0的解;
(2)若函数f(x)在(0,2)上有两个不同的零点x1,x2,求k的取值范围;并证明:
+
<4.
(1)若k=2,求方程f(x)=0的解;
(2)若函数f(x)在(0,2)上有两个不同的零点x1,x2,求k的取值范围;并证明:
| 1 |
| x1 |
| 1 |
| x2 |
考点:函数零点的判定定理,根的存在性及根的个数判断
专题:计算题,证明题,函数的性质及应用
分析:(1)k=2时,f(x)=|x2-1|+x2+2x,从而讨论求方程f(x)=0的解;
(2)不妨设0<x1<x2<2,则化简f(x)=|x2-1|+x2+kx=
;从而可确定0<x1<1≤x2<2;从而可得kx1+1=0,2x2+kx-1=0;从而求k的取值范围并证明
+
<4.
(2)不妨设0<x1<x2<2,则化简f(x)=|x2-1|+x2+kx=
|
| 1 |
| x1 |
| 1 |
| x2 |
解答:
解:(1)k=2时,f(x)=|x2-1|+x2+2x,
当|x|≥1时,f(x)=2x2+2x-1,
由f(x)=2x2+2x-1=0得,
x=
,x=
(舍去),
当|x|<1时,f(x)=2x+1,
由2x+1=0得x=-
;
故当k=2时,方程f(x)=0的解是x=
或x=-
.
(2)不妨设0<x1<x2<2,
∵f(x)=|x2-1|+x2+kx=
;
若x1,x2∈[1,2),与x1x2=-
矛盾,
则0<x1<1≤x2<2;
则kx1+1=0 ①,2x2+kx-1=0 ②;
由①得:k=-
<-1,
由②得:k=
-2x2∈(-
,-1];
∴k的取值范围是(-
,-1);
联立①、②消去k得:
2
-
x2-1=0;
即
+
<2x2<4.
当|x|≥1时,f(x)=2x2+2x-1,
由f(x)=2x2+2x-1=0得,
x=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
当|x|<1时,f(x)=2x+1,
由2x+1=0得x=-
| 1 |
| 2 |
故当k=2时,方程f(x)=0的解是x=
-1-
| ||
| 2 |
| 1 |
| 2 |
(2)不妨设0<x1<x2<2,
∵f(x)=|x2-1|+x2+kx=
|
若x1,x2∈[1,2),与x1x2=-
| 1 |
| 2 |
则0<x1<1≤x2<2;
则kx1+1=0 ①,2x2+kx-1=0 ②;
由①得:k=-
| 1 |
| x1 |
由②得:k=
| 1 |
| x2 |
| 7 |
| 2 |
∴k的取值范围是(-
| 7 |
| 2 |
联立①、②消去k得:
2
| x | 2 2 |
| 1 |
| x1 |
即
| 1 |
| x1 |
| 1 |
| x2 |
点评:本题考查了函数的性质的判断与应用,同时考查了分段函数的应用,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
已知双曲线与抛物线y2=8x有公共的焦点,且双曲线的离心率为2,则该双曲线的标准方程为( )
A、x2-
| ||
B、y2-
| ||
C、x2-
| ||
D、y2-
|
定义域是R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=
,若x∈(-4,-2]时,f(x)≤
-
有解,则实数t的取值范围是( )
|
| t |
| 4 |
| 1 |
| 2t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
下列两个程序(1)和(2)的运行的结果i分别是( )

| A、7,7 | B、7,6 |
| C、6,7 | D、6,6 |
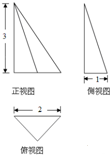 某三棱锥的三视图如图所示,其正视图和侧视图都是直角三角形,则该三棱锥的体积等于( )
某三棱锥的三视图如图所示,其正视图和侧视图都是直角三角形,则该三棱锥的体积等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
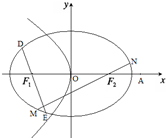 设椭圆C1:
设椭圆C1:
