题目内容
11.若定义在(-1,1)上的奇函数f(x)满足当x∈(0,1)时,f(x)=$\frac{{2}^{x}}{{4}^{x}+1}$.(1)求f(x)在(-1,1)上的解析式;
(2)试判断f(x)在(0,1)上的单调性,并给予证明;
(3)当a为何值时,关于方程f(x)=a在(0,1)上有实数解?
分析 (1)根据奇函数的性质分别求出f(x)在(-1,0)和x=0时的解析式,再写出分段函数;
(2)求出f(x)在(0,1)上的导数,判断导数的符号,得出结论;
(3)求出f(x)在(0,1)上的值域,得出a的范围.
解答 解:(1)令-1<x<0,则0<-x<1,
∴f(-x)=$\frac{{2}^{-x}}{{4}^{-x}+1}$=$\frac{{2}^{x}}{1+{4}^{x}}$,
∵f(x)是奇函数,∴f(x)=-f(-x)=-$\frac{{2}^{x}}{1+{4}^{x}}$,
∵f(x)是奇函数,∴f(0)=0,
∴f(x)=$\left\{\begin{array}{l}{-\frac{{2}^{x}}{1+{4}^{x}},-1<x<0}\\{0,x=0}\\{\frac{{2}^{x}}{1+{4}^{x}},0<x<1}\end{array}\right.$.
(2)当x∈(0,1)时,f(x)=$\frac{{2}^{x}}{1+{4}^{x}}$=$\frac{1}{\frac{1}{{2}^{x}}+{2}^{x}}$,设0<x1<x2<1,
则f(x1)-f(x2)=$\frac{1}{\frac{1}{{2}^{{x}_{1}}}+{2}^{{x}_{1}}}$-$\frac{1}{\frac{1}{{2}^{{x}_{2}}}+{2}^{{x}_{2}}}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}+\frac{1}{{2}^{{x}_{2}}}-\frac{1}{{2}^{{x}_{1}}}}{(\frac{1}{{2}^{{x}_{1}}}+{2}^{{x}_{1}})(\frac{1}{{2}^{{x}_{2}}}+{2}^{{x}_{2}})}$=$\frac{({2}^{{x}_{2}}-{2}^{{x}_{1}})(1-\frac{1}{{2}^{{x}_{1}}{2}^{{x}_{2}}})}{(\frac{1}{{2}^{{x}_{1}}}+{2}^{{x}_{1}})(\frac{1}{{2}^{{x}_{2}}}+{2}^{{x}_{2}})}$.
∵0<x1<x2<1,∴2${\;}^{{x}_{2}}$>2${\;}^{{x}_{1}}$>1,∴2${\;}^{{x}_{2}}$-2${\;}^{{x}_{1}}$>0,1-$\frac{1}{{2}^{{x}_{1}}{2}^{{x}_{2}}}$>0,$\frac{1}{{2}^{{x}_{1}}}+{2}^{{x}_{1}}$>0,$\frac{1}{{2}^{{x}_{2}}}+{2}^{{x}_{2}}$>0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴f(x)在(0,1)上是减函数.
(3)∵f(x)在(0,1)上是减函数,∴当x∈(0,1)时,$\frac{2}{5}$<f(x)<$\frac{1}{2}$,
当$\frac{2}{5}$<a<$\frac{1}{2}$时,方程f(x)=a在(0,1)上有实数解.
点评 本题考查了奇函数的性质,函数单调性的判断,函数的值域,属于中档题.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
| A. | -$\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | -$\frac{12}{5}$ | D. | $\frac{12}{5}$ |
| A. | 当m∈$(\frac{2}{3},+∞)$时,函数h(x)无零点 | |
| B. | 当m∈$(-∞,\frac{2}{3})$时,函数h(x)恰有一个零点 | |
| C. | 当m∈$[0,\frac{2}{3}]$时,函数h(x)恰有两个零点 | |
| D. | 当m∈$(-\frac{2}{3},\frac{2}{3})$时,函数h(x)恰有三个零点 |
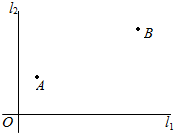 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.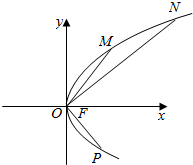 已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.
已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.