题目内容
8.设数列{an}为等差数列,Sn为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为( )| A. | 3 | B. | 4 | C. | -7 | D. | -5 |
分析 利用等差数列的通项公式与求和公式与不等式的性质即可得出.
解答 解:∵S4≥10,S5≤15,
∴a1+a2+a3+a4≥10,a1+a2+a3+a4+a5≤15,
∴a5≤5,a3≤3,
即:a1+4d≤5,a1+2d≤3,
两式相加得:2(a1+3d)≤8,
∴a4≤4,
故选:B.
点评 本题考查了等差数列的通项公式与求和公式与不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.若直线ax+by+1=0(a>0,b>0)把圆(x+4)2+(y+1)2=16分成面积相等的两部分,则$\frac{1}{2a}+\frac{2}{b}$的最小值为( )
| A. | 10 | B. | 8 | C. | 5 | D. | 4 |
17.复数$\frac{2}{i(3-i)}$=( )
| A. | $\frac{1-3i}{5}$ | B. | $\frac{1+3i}{5}$ | C. | $\frac{3+i}{5}$ | D. | $\frac{3-i}{5}$ |
18.已知2sinx=1+cosx,则$cot\frac{x}{2}$=( )
| A. | 2 | B. | 2或$\frac{1}{2}$ | C. | 2或0 | D. | $\frac{1}{2}$或0 |
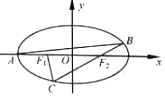 如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.
如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.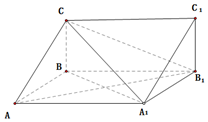 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.